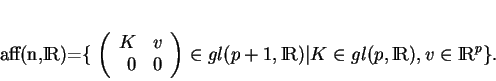La première montre que l'on peut ramener l'étude de l'espace tangent
en un point quelconque de ![]() à l'espace tangent en
à l'espace tangent en ![]() .
.
Soit en effet un élément
Pour simplifier les écritures, nous poserons
![]() .
.
En utilisant la Proposition 23, il est facile
d'identifier cet espace pour les groupes donnés en exemple plus haut.
Pour ceux-ci,
![]() porte généralerment le même nom que le groupe
mais écrit en minuscules.
En particulier,
porte généralerment le même nom que le groupe
mais écrit en minuscules.
En particulier,
![]() est l'espace tangent à
est l'espace tangent à
![]() en
en
![]() . C'est aussi celui de
. C'est aussi celui de
![]() .
Pour
.
Pour
![]() , c'est l'ensemble
, c'est l'ensemble
![]() des matrices de trace nulle. Pour
des matrices de trace nulle. Pour ![]() et
et ![]() , on
obtient le même espace,
ensemble
, on
obtient le même espace,
ensemble
![]() des
matrices antisymétriques. Les analogues complexes
des
matrices antisymétriques. Les analogues complexes ![]() et
et ![]() ont pour espace
tangent en l'unité l'espace
ont pour espace
tangent en l'unité l'espace
![]() des
matrices antihermitiennes et l'espace
des
matrices antihermitiennes et l'espace ![]() des matrices
antihermitiennes de trace nulle
respectivement. Enfin, le groupe affine
des matrices
antihermitiennes de trace nulle
respectivement. Enfin, le groupe affine
![]() est tangent en
l'unité à l'espace
est tangent en
l'unité à l'espace