



suivant: 5.2.2.2 Algèbres de Lie
monter: 5.2.2 L'algèbre de Lie
précédent: 5.2.2 L'algèbre de Lie
Table des matières
Un espace vectoriel 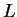 muni d'une application bilinéaire
antisymétrique
muni d'une application bilinéaire
antisymétrique
![$ (x,y)\mapsto [x,y]$](img956.gif) vérifiant l'identité de
Jacobi
est une algèbre de Lie. Le commutateur de matrices vérifie
cette identité. L'espace vectoriel
vérifiant l'identité de
Jacobi
est une algèbre de Lie. Le commutateur de matrices vérifie
cette identité. L'espace vectoriel
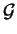 est donc une algèbre de Lie.
C'est l'algèbre de
Lie du groupe
est donc une algèbre de Lie.
C'est l'algèbre de
Lie du groupe 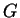 .
.
La correspondance entre un groupe et son algèbre de lie est
extrêmement riche de propriétés. Son étude sort du cadre du présent
texte. Disons
simplement, en gros, qu'un groupe est déterminé au moins au voisinage
de l'élément neutre par son algèbre de Lie et que toutes les algèbres
de Lie de dimension
finie sont (isomorphes à) des algèbres de Lie de groupes.
Le crochet de Lie ![$ [ \ ,\ ]$](img958.gif) d'une algèbre de lie
d'une algèbre de lie 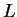 de
dimension finie
de
dimension finie 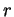 est caractérisé par ses valeurs sur les éléments
d'une base
est caractérisé par ses valeurs sur les éléments
d'une base
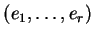 de
de 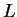 , c'est-à-dire par les nombres
, c'est-à-dire par les nombres 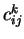 ,
appelés constantes de structure, exprimant
,
appelés constantes de structure, exprimant ![$ [e_i,e_j]$](img961.gif) selon
cette base:
selon
cette base:
Si tous les crochets de Lie sont nuls, l'algèbre est dite commutative ou abélienne.
C'est évidemment le cas des algèbres de Lie de dimension  , à cause
de l'antisymétrie du crochet de Lie.
, à cause
de l'antisymétrie du crochet de Lie.




suivant: 5.2.2.2 Algèbres de Lie
monter: 5.2.2 L'algèbre de Lie
précédent: 5.2.2 L'algèbre de Lie
Table des matières
![]() d'une algèbre de lie
d'une algèbre de lie ![]() de
dimension finie
de
dimension finie ![]() est caractérisé par ses valeurs sur les éléments
d'une base
est caractérisé par ses valeurs sur les éléments
d'une base
![]() de
de ![]() , c'est-à-dire par les nombres
, c'est-à-dire par les nombres ![]() ,
appelés constantes de structure, exprimant
,
appelés constantes de structure, exprimant ![]() selon
cette base:
selon
cette base:
![$\displaystyle [e_i,e_j]=\sum_k c^k_{ij}e_k.
$](img962.gif)