suivant: 5.2.2.4 Opérateurs différentiels homogènes
monter: 5.2.2 L'algèbre de Lie
précédent: 5.2.2.2 Algèbres de Lie
Table des matières
L'algèbre de
Lie de Heisenberg 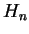 est de dimension
est de dimension 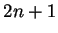 et admet une base
et admet une base
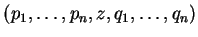 dans laquelle le crochet de Lie
est caractérisé par le fait que le crochet de Lie
dans laquelle le crochet de Lie
est caractérisé par le fait que le crochet de Lie ![$ [z,.]$](img987.gif) par
par 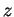 est
nul et par
Si on représente par
est
nul et par
Si on représente par 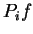 la dérivée de
la dérivée de
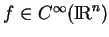 par
rapport à la variable
par
rapport à la variable 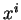 , par
, par 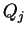 le produit
le produit 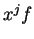 et par
et par 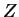 l'indentité de
l'indentité de
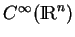 dans lui-même, alors,
dans l'ensemble des applications linéaires de cet espace dans
lui-même, les commutateurs de
ces applications linéaires vérifient les mêmes relations que la base
de
dans lui-même, alors,
dans l'ensemble des applications linéaires de cet espace dans
lui-même, les commutateurs de
ces applications linéaires vérifient les mêmes relations que la base
de 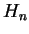 ci-dessus.
ci-dessus.
Le lecteur vérifiera à titre d'exercice que l'algèbre de Lie du
groupe des matrices
est isomorphe à l'algèbre 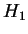 .
.