



suivant: 3.3.3 Orientation en dimension
monter: 3.3.2 Orientation d'un plan
précédent: 3.3.2 Orientation d'un plan
Table des matières
Supposons que 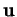 et
et 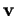 sont linéairement indépendants, de même que
sont linéairement indépendants, de même que 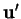 et
et 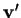 .
Notons
.
Notons 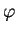 l'angle non orienté entre
l'angle non orienté entre 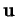 et
et 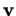 et
et 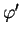 celui séparant
celui séparant 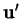 de
de 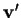 .
.
Proposition 3.3.1
Si
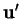
est orthogonal à
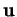
et
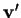
à
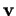
, alors
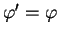
si
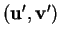
a même orientation que
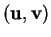
et
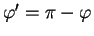
sinon.
Preuve. Quitte à les diviser par leur longueurs, on peut supposer les vecteurs normés, ce qui ne change pas les orientations considérées.
Notons 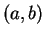 les composantes de
les composantes de 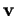 dans la base orthonormée
dans la base orthonormée
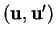 . Celles de
. Celles de 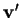 sont de la forme
sont de la forme 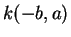 , avec
, avec 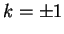 puisque
puisque 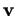 et
et 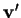 sont de longueur
sont de longueur 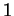 . On a
D'où le résultat car
. On a
D'où le résultat car
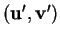 a même orientation que
a même orientation que
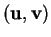 si et seulement si
si et seulement si 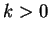 .
.
2002-12-17