... (^0.1

Si l'on doit pouvoir aussi bien représenter les nombres entiers que les réels ou les complexes, nous nous limiterons ici aux entiers positifs ou nuls.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... (^0.2

A un décalage d'indice près, c'est la suite de Fibonacci 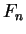$F_n$. On a $f_n=F_{n+1}$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

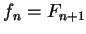... (^0.3

Cela sera laissé à titre d'exercice.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... forme(^0.4

Le nombre 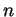$n$ admet plusieurs décompositions de cette forme. Il est donc nécessaire de préciser celle avec laquelle on convient de le représenter, par exemple au moyen d'un algorithme permettant de la construire.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... nécessaire(^0.5

Elle n'est pas suffisante. Le problème de trouver une telle condition est partiellement résolu. C'est une question difficile.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...(^0.6

Un entier algébrique est un zéro d'un polynôme à coefficients entiers dont le coefficient du terme dominant est égal à 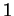$1$. Un tel nombre annule un polynôme de degré minimum, dont les racines en sont les conjugués.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...(^0.7

Il est possible que 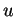$u$ soit vide. Dans ce cas, 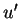$u'$ ne l'étant pas, $b'>b=0$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

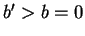... (^0.8

La vérification du cas où 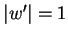$\vert w'\vert=1$ est immédiate

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... (^0.9

La fonction 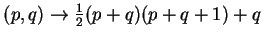$(p,q)\to \frac{1}{2}(p+q)(p+q+1)+q$ est la fonction de Peano, bien connue en théorie des fonctions récursives; elle est primitive récursive.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... trivial(^0.10

Des entiers distincts 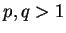$p, q>1$ sont multiplicativement indépendants si aucune puissance positive de l'un n'est égal à une puissance positive de l'autre.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... impair(^0.11

L'addition ne préserve donc pas le caractère reconnaissable car sinon, la multiplication par 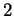$2$ le ferait aussi.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...(^0.12

On peut par exemple prendre l'automate minimal de 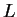$L$. A ce stade, 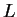$L$ n'est pas supposé régulier

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... (^0.13

Lorsque le langage 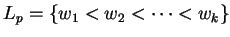$L_p=\{w_1<w_2<\cdots<w_k\}$ est fini, il ne donne pas lieu à un système de numération mais 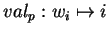$val_p:w_i\mapsto i$ est bien défini.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...val)(^0.14

La proposition permet d'ailleurs de démontrer cette formule.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...(^0.15

C'est-à-dire périodique à partir d'un certain rang.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... long(^0.16

Par exemple $\vert w\vert>N$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

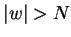... l'alphabet(^0.17

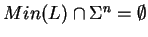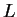On pose $Min(L)\cap\Sigma^n=\emptyset$ si $L$ n'a pas de mots de longueur 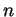$n$. Remarque analogue pour $Max(L)$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

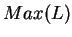... Fermat(^0.18

Si 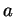$a$ n'est pas multiple du nombre premier 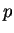$p$, alors $a^{p-1}\equiv 1 \mod p$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

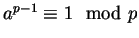... aussi(^0.19

Avec, pour les besoins de cette démonstration, $\Sigma=\{0,\ldots,k-1\}$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

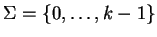... également(^0.20

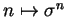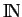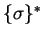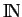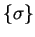La correspondance $n\mapsto \sigma^n$ identifie ${\rm I\!N}$ à $\{\sigma\}^*$ et, par conséquent, les unions finies de progressions arithmétiques de ${\rm I\!N}$ aux parties régulières de $\{\sigma\}$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.