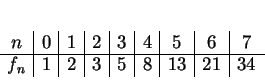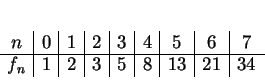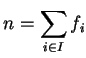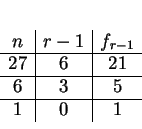

suivant: 0.1.3 Une généralisation
monter: 0.1 Les systèmes de
précédent: 0.1.1 introduction
Posons
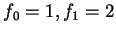 et, pour
et, pour 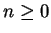 ,
,
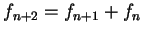 (0.2).
Voici les premiers éléments de cette suite.
On peut vérifier que tout entier positif
(0.2).
Voici les premiers éléments de cette suite.
On peut vérifier que tout entier positif 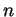 s'écrit, de manière unique, sous la forme
où dans
s'écrit, de manière unique, sous la forme
où dans 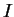 , il n'y a pas d'éléments consécutifs.
Une façon simple de s'en convaincre est de construire la décomposition de
, il n'y a pas d'éléments consécutifs.
Une façon simple de s'en convaincre est de construire la décomposition de 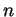 par récurrence:
par récurrence:
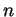 est encadré par deux éléments consécutifs de la suite
On place
est encadré par deux éléments consécutifs de la suite
On place 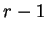 dans
dans 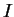 puis on recommence en substituant
puis on recommence en substituant 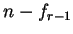 à
à 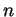 .
Il faut vérifier qu'à la fin, il n'y aura pas d'éléments consécutifs dans
.
Il faut vérifier qu'à la fin, il n'y aura pas d'éléments consécutifs dans 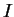 ainsi que l'unicité de la décompostion (0.3).
Voici ce que cela donne pour
ainsi que l'unicité de la décompostion (0.3).
Voici ce que cela donne pour 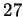 :
On peut donc représenter
:
On peut donc représenter 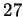 par
par 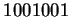 , les
, les 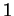 occupant les positions dont les rangs comptés de droite à gauche et à partir de zéro, sont les éléments de
occupant les positions dont les rangs comptés de droite à gauche et à partir de zéro, sont les éléments de
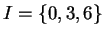 . En codant de la même façon tous les entiers positifs et en représentant zéro par 0, on obtient un système de numération, le système de Zeckendorf. Le langage de numération associé est écrit sur l'alphabet
. En codant de la même façon tous les entiers positifs et en représentant zéro par 0, on obtient un système de numération, le système de Zeckendorf. Le langage de numération associé est écrit sur l'alphabet 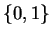 . Il est régulier: c'est l'intersection du langage contenant 0 et les mots commençants par
. Il est régulier: c'est l'intersection du langage contenant 0 et les mots commençants par  et du langage formé des mots ne contenant pas le facteur
et du langage formé des mots ne contenant pas le facteur 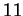 , qui sont tous les deux réguliers.
, qui sont tous les deux réguliers.


suivant: 0.1.3 Une généralisation
monter: 0.1 Les systèmes de
précédent: 0.1.1 introduction
2002-12-17