

suivant: Représentation monotone
monter: 0.1.3 Une généralisation
précédent: Alphabet fini
Nous ne donnerons pas de conditions nécessaires et suffisantes, en terme des 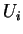 , sous lesquelles le langage de numération associé à une suite
, sous lesquelles le langage de numération associé à une suite 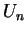 dont le quotient
dont le quotient
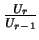 est borné, est régulier sur l'alphabet des chiffres. Voici au moins une condition nécessaire(0.5).
est borné, est régulier sur l'alphabet des chiffres. Voici au moins une condition nécessaire(0.5).
Proposition 0.1.2
Si le langage de numération associé à une suite strictement croissante d'entiers

, telle que
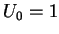
et
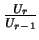
est borné est régulier, alors
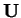
solution d'une équation de récurrence linéaire à coefficients constants et entiers.
Preuve. En effet, il résulte de la définition de la représentation d'un nombre 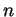 que celle-ci comporte
que celle-ci comporte 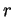 lettres exactement si et seulement si
lettres exactement si et seulement si
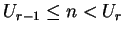 . Il y a donc
. Il y a donc
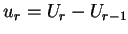 mots de longueur
mots de longueur 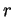 dans le langage de numération associé à
dans le langage de numération associé à  . S'il est régulier, alors la suite des
. S'il est régulier, alors la suite des  est solution d'une équation de récurrence linéaire à coefficients entiers et constants. Il en va donc de même de
est solution d'une équation de récurrence linéaire à coefficients entiers et constants. Il en va donc de même de 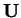 .
.
Pour la numération de position classique en base 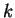 , la relation de récurrence est tout simplement
, la relation de récurrence est tout simplement
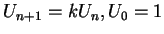 .
.
Les systèmes basés sur un nombre de Pisot ont un langage de numération régulier. Nous ne vérifierons pas cette propriété qui donne une collection importante de systèmes pour lesquels la réciproque de la proposition précédente est donc vraie. Pour rappel, un nombre de Pisot est un entier algébrique plus grand que 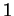 et dont les conjugués sont de module plus petit que
et dont les conjugués sont de module plus petit que 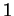 (0.6).
(0.6).
Les entiers plus grands que 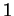 sont des nombres de Pisot; le nombre d'or
sont des nombres de Pisot; le nombre d'or
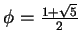 en est un aussi. Son polynôme minimum est
en est un aussi. Son polynôme minimum est 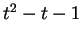 . Son second zéro est
. Son second zéro est
 .
.


suivant: Représentation monotone
monter: 0.1.3 Une généralisation
précédent: Alphabet fini
2002-12-17
![]() , la relation de récurrence est tout simplement
, la relation de récurrence est tout simplement
![]() .
.
![]() et dont les conjugués sont de module plus petit que
et dont les conjugués sont de module plus petit que ![]() (0.6).
(0.6).
![]() sont des nombres de Pisot; le nombre d'or
sont des nombres de Pisot; le nombre d'or
![]() en est un aussi. Son polynôme minimum est
en est un aussi. Son polynôme minimum est ![]() . Son second zéro est
. Son second zéro est
![]() .
.