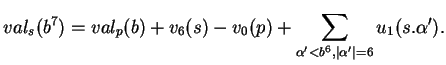

suivant: 0.2.4 Les progressions arithmétiques
monter: 0.2 Systèmes abstraits
précédent: 0.2.2 Quelques questions
Nous allons montrer comment calculer la fonction 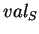 d'un système de numération abstrait
d'un système de numération abstrait
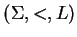 au moyen d'un automate déterministe
au moyen d'un automate déterministe
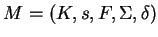 acceptant le langage
acceptant le langage 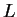 (0.12).
Pour chaque état
(0.12).
Pour chaque état 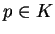 de
de 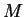 , notons
, notons
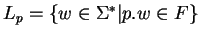 le langage formé des mots acceptés par
le langage formé des mots acceptés par 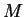 à partir de
à partir de 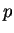 et
et 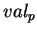 la fonction valeur relative au système
la fonction valeur relative au système
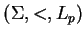 (0.13).
Rappelons que, pour tout langage
(0.13).
Rappelons que, pour tout langage 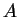 , on désigne par
, on désigne par 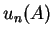 le nombre de mots de longueur
le nombre de mots de longueur 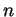 de
de 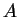 et par
et par 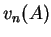 le nombre de mots de A de longueur inférieure ou égale à
le nombre de mots de A de longueur inférieure ou égale à 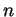 . Nous poserons
. Nous poserons
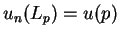 et
et
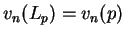 .
.
L'automate minimal du langage 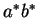 , représenté ci-dessous, possède trois états:
, représenté ci-dessous, possède trois états: 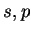 et
et 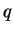 .
Les langages associés sont
.
Les langages associés sont
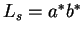 ,
, 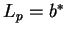 et
et
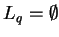 .
.
Figure:
L'automate minimal de 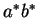 .
.
|
|
On a donc
Preuve. Le nombre 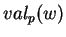 est le nombre de mots de
est le nombre de mots de 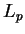 qui sont plus petits que
qui sont plus petits que 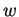 .
Ceux-ci se répartissent en trois ensembles. Le premier contient les mots de
.
Ceux-ci se répartissent en trois ensembles. Le premier contient les mots de 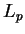 qui sont plus courts que
qui sont plus courts que 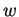 . Il y en a
. Il y en a
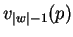 . Dans le second, nous plaçons les mots de
. Dans le second, nous plaçons les mots de 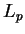 , de longueur
, de longueur 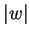 et admettant le préfixe
et admettant le préfixe 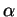 . Ces mots sont ceux de la forme
. Ces mots sont ceux de la forme
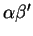 , où
, où 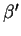 appartient à
appartient à
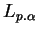 , est de même longueur que
, est de même longueur que 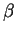 mais est plus petit que lui. Il y en a
mais est plus petit que lui. Il y en a
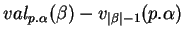 . Le dernier est constitué des mots de
. Le dernier est constitué des mots de 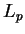 , de même longueur que
, de même longueur que 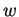 mais ne commençant pas par
mais ne commençant pas par 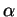 . Ces mots s'écrivent
. Ces mots s'écrivent
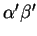 , avec
, avec
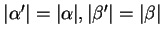 ,
,
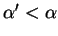 et
et
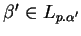 .
.
Illustrons cette proposition pour calculer
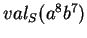 sans utiliser la formule (
sans utiliser la formule (![[*]](crossref.gif) )(0.14).
Posons
)(0.14).
Posons 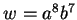 ,
,
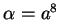 et
et 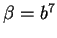 .
Il vient,
.
Il vient,
(il n'y a pas de mots 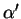 de longueur
de longueur 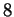 plus petits que
plus petits que
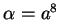 ).
Appliquons encore la proposition pour déterminer
).
Appliquons encore la proposition pour déterminer
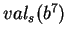 en posant cette fois
en posant cette fois
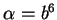 et
et 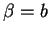 :
Les mots
:
Les mots 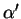 de longueur
de longueur 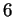 plus petits que
plus petits que 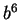 sont
sont 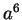 , pour lequel
, pour lequel
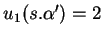 , et les
, et les 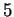 mots
mots
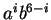 ,
,
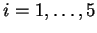 , pour lesquels
, pour lesquels
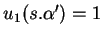 .
Au total,
.
.
Au total,
.


suivant: 0.2.4 Les progressions arithmétiques
monter: 0.2 Systèmes abstraits
précédent: 0.2.2 Quelques questions
2002-12-17
![]() , représenté ci-dessous, possède trois états:
, représenté ci-dessous, possède trois états: ![]() et
et ![]() .
Les langages associés sont
.
Les langages associés sont
![]() ,
, ![]() et
et
![]() .
.
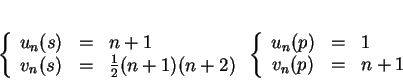
![]() sans utiliser la formule (
sans utiliser la formule (![[*]](crossref.gif) )(0.14).
Posons
)(0.14).
Posons ![]() ,
,
![]() et
et ![]() .
Il vient,
.
Il vient,