0.2.5 Premiers et derniers mots de chaque longueur

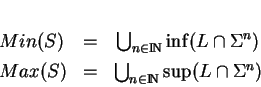
Soit un système de numération abstrait $S=(\Sigma,<,L)$. On désigne par $Min(S)$ l'ensemble des plus petit mots de $L$ de chaque longueur, et par $Max(S)$ celui des plus grands mots de L de chaque longueur:

$$% latex2html id marker 3133\begin{array}{lcc} Min(S)&=&\bi... ...S)&=&\bigcup_{n\in {\rm I\!N}}\sup (L\cap \Sigma^n) \end{array}$$

On note aussi $Min(L)$ et $Max(L)$ ces langages lorsqu'il n'y pas d'ambiguité sur l'ordre des lettres de l'alphabet(^0.17).

Proposition 0.2.4   Soit un système de numération abstrait $S=(\Sigma,<,L)$ dont le langage $L$ est régulier. Les langages $Min(S)$ et $Max(S)$ sont réguliers

Preuve. Nous faisons la démonstration pour $Min(L)$. Elle est facile à adapter pour $Max(L)$. Nous allons décrire les états $w^{-1}.Min(L)$ de l'automate minimal de $Min(L)$ au moyen des états $v^{-1}.L$ de celui de $L$ d'une manière qui fait voir clairement que le premier est fini s'il en va de même du second.

Soit $w\in\Sigma^*$. Notons $I_w$ l'ensemble des entiers positifs $i$ vérifiant

$$v<w\ \& \ \vert v\vert=\vert w\vert \Longrightarrow (v^{-1}.L)\cap\Sigma^i=\emptyset.$$

On a alors

$$w^{-1}.Min(L)=Min(w^{-1}.L)\cap\bigcup_{i\in I_w}\Sigma^i.$$ (0.4)

Si l'automate minimal de $L$ est fini, il n'y a qu'un nombre fini d'ensembles $I_w$ et, dès lors, le membre de droite de () ne prend également qu'un nombre fini de valeurs.

L'égalité () est aisée à vérifier: l'appartenance de $u$ à $Min(w^{-1}.L)$ signifie que $wu$ est plus petit ou égal au mots de $L$ admettant le préfixe $w$; le fait que $\vert u\vert\in I_w$ signifie quant à lui que $L$ ne contient pas de mot de longueur $\vert wu\vert$ admettant un préfixe de longueur $\vert w\vert$ mais plus petit que $w$ dans l'ordre généalogique.$\qed$

Le plus petit mot de longueur $n+1$ de $L$ porte le numéro $v_n(L)$. Par conséquent,

Corollaire 0.2.5   Soit un système de numération abstrait $S=(\Sigma,<,L)$ dont le langage $L$ est régulier. L'ensemble $\{v_n(L)\vert n\in{\rm I\!N}\}$ est $S$-reconnaissable.

L'ensemble des entiers $\frac{1}{2}(n+1)(n+2), n\in{\rm I\!N},$ est donc $S$-reconnaissable pour les systèmes dont le langage est $a^*b^*$. On peut perfectionner cet exemple et obtenir un système dans lequel l'ensemble des carrés parfaits est reconnaissable. Il suffit de remplacer $a^*b^*$ par le langage $a^*b^*\cup a^*c^*$. Celui-ci compte en effet $2n+1$ mots de longueur $n$ si bien que $v_n(L)$ vaut alors $n^2$. Nous allons voir à la section suivante que l'ensemble des carrés parfaits n'est reconnaissable dans aucun des systèmes de numération classiques.