

suivant: 0.2.2 Quelques questions
monter: 0.2 Systèmes abstraits
précédent: 0.2 Systèmes abstraits
Nous allons voir quelles sont ces fonctions dans le cas du système
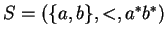 , où
, où 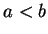 . Commençons par
. Commençons par 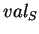 qui possède une expression simple à formuler (0.9):
qui possède une expression simple à formuler (0.9):
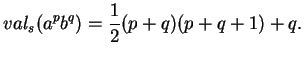 |
(0.3) |
Rangés dans l'ordre généalogique, les mots de longueur 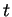 de
de 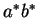 sont en effet les
sont en effet les 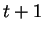 mots
et le mot
mots
et le mot
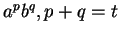 , est le
, est le 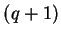 -ième d'entre eux.
Ceux qui les précèdent sont en nombre
-ième d'entre eux.
Ceux qui les précèdent sont en nombre
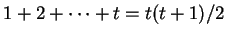 .
Le numéro de
.
Le numéro de 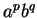 a donc bien la valeur de
a donc bien la valeur de
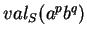 indiquée ci-dessus.
indiquée ci-dessus.
Pour calculer 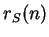 , il faut d'abord déterminer sa longueur. Elle est donnée par
, il faut d'abord déterminer sa longueur. Elle est donnée par
On obtient ensuite 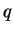 et
et 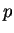 par les formules
par les formules
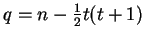 et
et 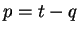 .
Vu le choix de
.
Vu le choix de 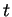 , on a en effet
, on a en effet
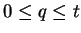 . De là,
. De là, 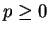 et, finalement,
et, finalement,
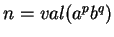 .
.
Ainsi, pour 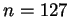 , comme
, comme
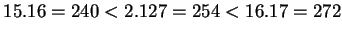 , il vient
, il vient 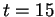 ,
, 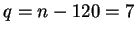 et
et 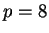 . Par conséquent
. Par conséquent
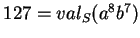 .
.
2002-12-17
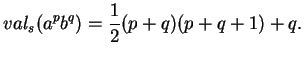
![]() , il faut d'abord déterminer sa longueur. Elle est donnée par
, il faut d'abord déterminer sa longueur. Elle est donnée par
![]() , comme
, comme
![]() , il vient
, il vient ![]() ,
, ![]() et
et ![]() . Par conséquent
. Par conséquent
![]() .
.