

suivant: 0.2.5 Premiers et derniers
monter: 0.2 Systèmes abstraits
précédent: 0.2.3 La fonction
Lemme 0.2.2
Soit un entier postif
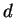
.
Si une suite d'entiers est solution d'une équation de récurrence linéaire à coefficients constants et entiers, alors la suite de ses restes par rapport à
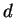
est ultimement périodique (
0.15).
Preuve. En effet, la suite des restes 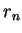 en question vérifie la même équation, modulo
en question vérifie la même équation, modulo 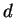 .
Notons
.
Notons 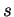 le degré de celle-ci. Il y a exactement
le degré de celle-ci. Il y a exactement 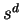 suites de
suites de 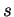 éléments parmi
éléments parmi
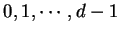 . Il y a donc deux indices
. Il y a donc deux indices 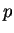 et
et 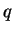 pour lesquels les
pour lesquels les 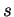 éléments consécutifs de la suite des
éléments consécutifs de la suite des 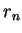 sont les mêmes à partir de
sont les mêmes à partir de 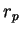 et
et 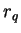 . On a donc
. On a donc
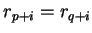 pour tout
pour tout 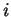 .
.
A titre d'illustration, voici les premiers restes modulo 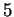 de la suite définissant la numération de Zeckendorf.
de la suite définissant la numération de Zeckendorf.
On y voit la répétition de 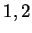 . Avec les notations de la démonstration,
. Avec les notations de la démonstration, 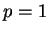 et
et 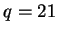 . Cette suite est donc périodique de période
. Cette suite est donc périodique de période 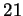 puisque chacun de ses éléments est la somme des deux précédents.
puisque chacun de ses éléments est la somme des deux précédents.
Proposition 0.2.3
Soit un système de numération abstrait
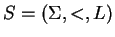
. Le langage
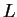
est régulier si et seulement si les progressions arithmétiques
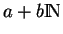
sont
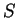
-reconnaissables.
Preuve. Comme
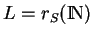 , il est régulier si les progressions arithmétiques sont
, il est régulier si les progressions arithmétiques sont 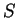 - reconnaissables.
Inversement, supposons que
- reconnaissables.
Inversement, supposons que 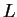 soit régulier et vérifions que
soit régulier et vérifions que
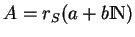 est régulier. On adopte les notations utilisées dans la Proposition
est régulier. On adopte les notations utilisées dans la Proposition ![[*]](crossref.gif) . En vertu du lemme précédent, les suites
. En vertu du lemme précédent, les suites 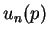 et
et 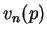 ,
, 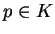 , sont ultimement périodiques modulo
, sont ultimement périodiques modulo 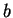 . Notons
. Notons 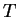 une période commune et
une période commune et 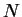 le maximum des longueurs des parties non périodiques. Les états de l'automate minimal de
le maximum des longueurs des parties non périodiques. Les états de l'automate minimal de 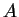 sont les ensembles
En vertu de la Proposition
sont les ensembles
En vertu de la Proposition ![[*]](crossref.gif) , pour
, pour 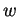 assez long(0.16),
assez long(0.16), 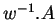 est donc un des ensembles de la forme
où
est donc un des ensembles de la forme
où 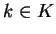 ,
,
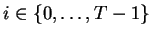 et, pour tout
et, pour tout 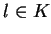 ,
,
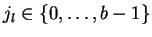 .
L'automate minimal de
.
L'automate minimal de 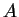 est donc fini.
est donc fini.
La propriété ci-dessus montre que, dans chaque numération de position classique, et en particulier en base 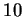 , les caractères de divisibilité sont caractérisés par des propriétés syntaxiques des mots représentant les nombres dans l'alphabet des chiffres. On peut donc détecter le fait qu'un nombre soit divisible par un autre par la forme de la suite des chiffres exprimant ce nombre, forme qui dépend du diviseur et de la base. La syntaxe des multiples de
, les caractères de divisibilité sont caractérisés par des propriétés syntaxiques des mots représentant les nombres dans l'alphabet des chiffres. On peut donc détecter le fait qu'un nombre soit divisible par un autre par la forme de la suite des chiffres exprimant ce nombre, forme qui dépend du diviseur et de la base. La syntaxe des multiples de 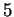 en base
en base 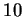 (se terminer par 0 ou
(se terminer par 0 ou 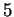 ) est extrêmement simple. Pour d'autres diviseurs ou d'autres bases, elle peut être trop compliquée pour être utilisée en pratique. C'est le cas du diviseur
) est extrêmement simple. Pour d'autres diviseurs ou d'autres bases, elle peut être trop compliquée pour être utilisée en pratique. C'est le cas du diviseur 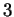 en base
en base 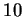 : les multiples de trois forment un langage régulier décrit par une expression régulière trop complexe pour que l'on puisse juger d'un simple coup d'oeil si un nombre est multiple de trois.
: les multiples de trois forment un langage régulier décrit par une expression régulière trop complexe pour que l'on puisse juger d'un simple coup d'oeil si un nombre est multiple de trois.


suivant: 0.2.5 Premiers et derniers
monter: 0.2 Systèmes abstraits
précédent: 0.2.3 La fonction
2002-12-17
![]() de la suite définissant la numération de Zeckendorf.
de la suite définissant la numération de Zeckendorf.
![[*]](crossref.gif) . En vertu du lemme précédent, les suites
. En vertu du lemme précédent, les suites ![[*]](crossref.gif) , pour
, pour 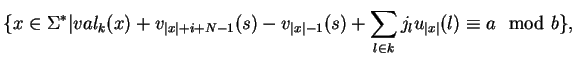
![]() , les caractères de divisibilité sont caractérisés par des propriétés syntaxiques des mots représentant les nombres dans l'alphabet des chiffres. On peut donc détecter le fait qu'un nombre soit divisible par un autre par la forme de la suite des chiffres exprimant ce nombre, forme qui dépend du diviseur et de la base. La syntaxe des multiples de
, les caractères de divisibilité sont caractérisés par des propriétés syntaxiques des mots représentant les nombres dans l'alphabet des chiffres. On peut donc détecter le fait qu'un nombre soit divisible par un autre par la forme de la suite des chiffres exprimant ce nombre, forme qui dépend du diviseur et de la base. La syntaxe des multiples de ![]() en base
en base ![]() (se terminer par 0 ou
(se terminer par 0 ou ![]() ) est extrêmement simple. Pour d'autres diviseurs ou d'autres bases, elle peut être trop compliquée pour être utilisée en pratique. C'est le cas du diviseur
) est extrêmement simple. Pour d'autres diviseurs ou d'autres bases, elle peut être trop compliquée pour être utilisée en pratique. C'est le cas du diviseur ![]() en base
en base ![]() : les multiples de trois forment un langage régulier décrit par une expression régulière trop complexe pour que l'on puisse juger d'un simple coup d'oeil si un nombre est multiple de trois.
: les multiples de trois forment un langage régulier décrit par une expression régulière trop complexe pour que l'on puisse juger d'un simple coup d'oeil si un nombre est multiple de trois.