suivant: 7.4.1 Cas des unions
monter: 7 Inégalité isopérimétrique
précédent: 7.3.3 Convexité & hessien
Table des matières
Cette section est consacrée à la démonstration de la Proposition 55.
Nous allons procéder en deux étapes.
La première consiste à vérifier l'inégalité de Brun-Minkowski lorsque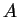 
et 
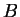sont des unions finies de semi-intervalles, par récurrence sur le nombre total de semi-intervalles composant 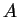et .
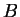La seconde montre comment passer d'unions de semi-intervalles à des compacts.
Sous-sections