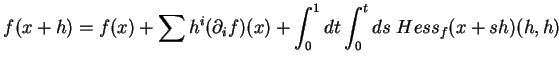 |
(7.2) |
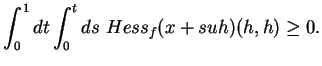
On retrouve en particulier l'étude de la concavité d'une fonction d'une variable réelle car, lorsque ![]() ,
,
![]() . On voit ainsi que
. On voit ainsi que ![]() est convexe si et seulement si
est convexe si et seulement si ![]() est partout positif ou nul. Par exemple,
est partout positif ou nul. Par exemple,
![]() est convexe. L'inégalité de Jensen donne alors
est convexe. L'inégalité de Jensen donne alors