7.4.1.1 Cas de semi-intervalles

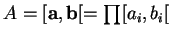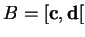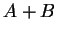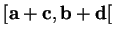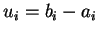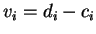Soient des semi-intervalles $A=[{\bf a},{\bf b}[=\prod [a_i,b_i[$ et $B=[{\bf c},{\bf d}[$. Comme on le vérifie facilement, $A+B$ est le semi-intervalle $[{\bf a}+{\bf c},{\bf b}+{\bf d}[$. Posons $u_i=b_i-a_i$ et $v_i=d_i-c_i$ et appliquons l'inégalité entre moyennes géométrique et arithmétique aux nombres 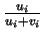$\frac{u_i}{u_i+v_i}$ puis aux nombres 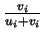$\frac{v_i}{u_i+v_i}$ pour obtenir

$$\sqrt[m]{\prod\frac{u_i}{u_i+v_i}}+\sqrt[m]{\prod\frac{v_i}{u_i+v_i}}\leq\frac{1}{m}\sum\frac{u_i}{u_i+v_i}+\frac{1}{m}\sum\frac{v_i}{u_i+v_i}=1.$$

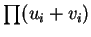En chassant le dénominateur $\prod(u_i+v_i)$, on obtient

$$\sqrt[m]{mes(A)}+\sqrt[m]{mes(B)}\leq\sqrt[m]{mes(A+B)}.$$ (7.3)