



suivant: 7.4.2 Cas de deux
monter: 7.4.1 Cas des unions
précédent: 7.4.1.1 Cas de semi-intervalles
Table des matières
On étend cette inégalité aux unions finies de semi-intervalles par récurrence sur le nombre total 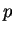 de semi-intervalles composant
de semi-intervalles composant 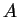 et
et 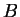 . Supposons qu'elle soit vraie lorsque
. Supposons qu'elle soit vraie lorsque 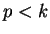 et vérifions-la pour
et vérifions-la pour 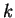 semi-intervalles (
semi-intervalles (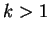 ).
).
Nous pouvons supposer que 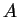 compte au moins deux semi-intervalles et trouver
compte au moins deux semi-intervalles et trouver 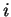 et
et 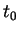 tels que chacun des ensembles
tels que chacun des ensembles
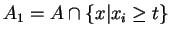 et
et
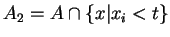 contienne un des semi-intervalles composant
contienne un des semi-intervalles composant 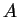 .
.
Nous pouvons alors partager 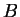 en deux unions de semi-intervalles
en deux unions de semi-intervalles
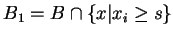 et
et
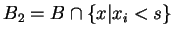 dans les mêmes proportions que
dans les mêmes proportions que 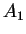 et
et 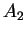 , c'est-à-dire de façon telle que
, c'est-à-dire de façon telle que
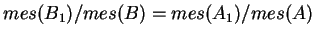 . Pour voir cela, il suffit d'observer que la fonction
. Pour voir cela, il suffit d'observer que la fonction
est continue. En effet, pour 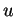 assez grand, elle vaut 0 et pour
assez grand, elle vaut 0 et pour 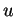 assez petit, elle vaut
assez petit, elle vaut  . Si elle est continue, elle prend donc toutes les valeurs comprises entre 0 et
. Si elle est continue, elle prend donc toutes les valeurs comprises entre 0 et  . La continuité de cette fonction résulte aisément du théorème de Lebesgue, une fois vérifié le fait que la fonction caractéristique de
. La continuité de cette fonction résulte aisément du théorème de Lebesgue, une fois vérifié le fait que la fonction caractéristique de
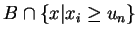 converge presque partout vers celle de
converge presque partout vers celle de
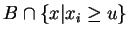 si
si 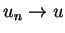 , ce qui est facile.
, ce qui est facile.
Il vient, en appliquant l'hypothèse de récurrence à 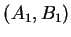 et à
et à 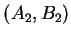 ,
,
Donc, puisque
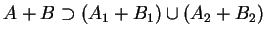 ,
,




suivant: 7.4.2 Cas de deux
monter: 7.4.1 Cas des unions
précédent: 7.4.1.1 Cas de semi-intervalles
Table des matières
![]() compte au moins deux semi-intervalles et trouver
compte au moins deux semi-intervalles et trouver ![]() et
et ![]() tels que chacun des ensembles
tels que chacun des ensembles
![]() et
et
![]() contienne un des semi-intervalles composant
contienne un des semi-intervalles composant ![]() .
.
![]() en deux unions de semi-intervalles
en deux unions de semi-intervalles
![]() et
et
![]() dans les mêmes proportions que
dans les mêmes proportions que ![]() et
et ![]() , c'est-à-dire de façon telle que
, c'est-à-dire de façon telle que
![]() . Pour voir cela, il suffit d'observer que la fonction
. Pour voir cela, il suffit d'observer que la fonction
![]() et à
et à ![]() ,
,
![$\displaystyle (\sqrt[m]{mes(A_i)}+\sqrt[m]{mes(B)\frac{mes(A_i)}{mes(A)}}\ )^m$](img1792.gif)
![$\displaystyle \frac{mes(A_i)}{mes(A)}(\sqrt[m]{mes(A)}+\sqrt[m]{mes(B)}\ )^m.$](img1793.gif)
![$\displaystyle (\frac{mes(A_1)}{mes(A)}+\frac{mes(A_2)}{mes(A)})(\sqrt[m]{mes(A)}+\sqrt[m]{mes(B)}\ )^m$](img1797.gif)