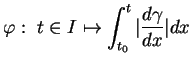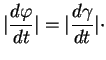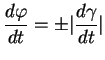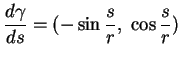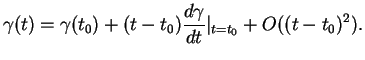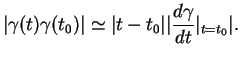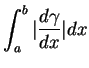suivant: 6.3.1.6 Courbe régulière par
monter: 6.3.1 Arc de courbe
précédent: 6.3.1.4 Orientation
Table des matières
Il est utile de trouver des vecteurs tangents à  qui soient normés.
Un paramétrage est naturel si
qui soient normés.
Un paramétrage est naturel si
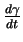 est normé pour tout
est normé pour tout 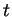 dans
dans 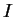 .
.
Proposition 6.3.4
Soient un arc paramétré de courbe

, un de ses paramétrages
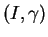
et
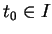
.
(i) La fonction
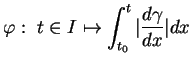 |
(6.4) |
est un changement de paramètres qui transforme
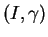
en un paramétrage naturel.
(ii) Deux paramétrages naturels de  diffèrent toujours par un changement
de paramètres de la forme
diffèrent toujours par un changement
de paramètres de la forme
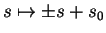 , où
, où 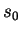 est une constante et où on choisit
est une constante et où on choisit
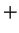 s'ils définissent la même orientation de
s'ils définissent la même orientation de  et
et 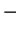 sinon.
sinon.
Preuve. La formule (25) montre que 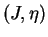 est naturel si et seulement si
Le point (i) en résulte car la fonction
est naturel si et seulement si
Le point (i) en résulte car la fonction 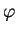 qui y est proposée possède cette propriété. Inversement,
si cette propriété est satisfaite, alors
le signe étant choisi selon l'orientation déterminée par
qui y est proposée possède cette propriété. Inversement,
si cette propriété est satisfaite, alors
le signe étant choisi selon l'orientation déterminée par 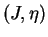 . D'où (ii).
. D'où (ii).
Exemple 6.3.5
Le cercle
Le paramétrage (23) du cercle centré en l'origine du repère et de rayon 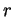 est naturel. En effet
est de longueur
est naturel. En effet
est de longueur 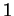 .
.
La formule de Taylor donne
La distance entre deux points voisins de  est donc approximativement
Lorsque
est donc approximativement
Lorsque 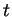 et
et 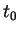 sont très proches, elle devrait intuitivement différer
très peu de la ``longueur" de la portion de
sont très proches, elle devrait intuitivement différer
très peu de la ``longueur" de la portion de  séparant ces points. Il est donc légitime de dire que, pour
séparant ces points. Il est donc légitime de dire que, pour 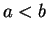 ,
représente la longueur de la portion de
,
représente la longueur de la portion de  délimitée par
délimitée par 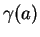 et
et 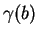 . Par exemple, on vérifie que la longueur de la circonférence et de
l'hélice (entre 0 et
. Par exemple, on vérifie que la longueur de la circonférence et de
l'hélice (entre 0 et 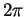 ) introduites plus haut sont respectivement
) introduites plus haut sont respectivement 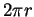 et
et
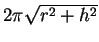 .
.
Quand 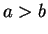 , cette intégrale est négative mais l'ordre des points
, cette intégrale est négative mais l'ordre des points
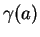 et
et 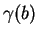 correspond à l'orientation opposée à celle définie par le paramétrage
correspond à l'orientation opposée à celle définie par le paramétrage
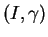 .
Finalement, (26) représente la longueur
d'arc parcourue en passant de
.
Finalement, (26) représente la longueur
d'arc parcourue en passant de  à
à 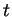 , comptée positivement lorsque
, comptée positivement lorsque 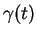 suit
suit
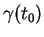 et négativement lorsqu'il le précède.
et négativement lorsqu'il le précède.
Le paramètre intervenant dans un paramétrage naturel s'appelle abscisse curviligne. Il est généralement représenté par la lettre 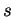 .
.




suivant: 6.3.1.6 Courbe régulière par
monter: 6.3.1 Arc de courbe
précédent: 6.3.1.4 Orientation
Table des matières
2002-12-17
![]() diffèrent toujours par un changement
de paramètres de la forme
diffèrent toujours par un changement
de paramètres de la forme
![]() , où
, où ![]() est une constante et où on choisit
est une constante et où on choisit
![]() s'ils définissent la même orientation de
s'ils définissent la même orientation de ![]() et
et ![]() sinon.
sinon.