



suivant: 1.2.2 Exemples
monter: 1.2 Applications différentiables
précédent: 1.2 Applications différentiables
Table des matières
Rappelons qu'une application
 d'un ouvert
d'un ouvert 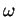 de
de
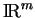 dans
dans
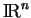 est différentiable en
est différentiable en
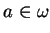 s'il existe une application linéaire
s'il existe une application linéaire
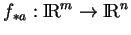 telle que
telle que
En prenant pour 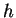 les vecteurs
les vecteurs
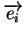 de la base canonique de
de la base canonique de
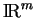 , on voit que si
, on voit que si  est différentiable en
est différentiable en  , ses dérivées partielles
, ses dérivées partielles
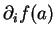 en
en  existent. De plus,
existent. De plus, 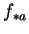 étant linéaire,
étant linéaire,
L'application 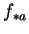 est donc représentée par la matrice
dans laquelle la ligne numéro
est donc représentée par la matrice
dans laquelle la ligne numéro 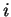 est formée des dérivées partielles de la composante
est formée des dérivées partielles de la composante 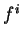 de numéro
de numéro 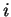 de
de  par rapports aux variables
par rapports aux variables
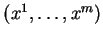 de
de
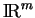 , calculées en
, calculées en  .
.
L'application 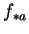 est l'application linéaire tangente de
est l'application linéaire tangente de  en
en  , ou encore, un peu abusivement, la différentielle de
, ou encore, un peu abusivement, la différentielle de  en
en  .
Notons que
.
Notons que 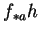 est la dérivée en
est la dérivée en 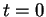 de la fonction
de la fonction
laquelle est définie dans un intervalle contenant 0. On appelle donc aussi 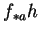 la dérivée de
la dérivée de  dans la direction de
dans la direction de 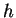 .
.
La remarque suivante résulte du théorème de dérivation des fonctions composées. Elle permet de vérifier facilement l'existence de l'application linéaire tangente: si les composantes
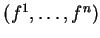 d'une fonction
d'une fonction
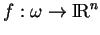 sont de classe
sont de classe 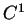 dans
dans 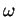 , alors
, alors  est différentiable.
est différentiable.




suivant: 1.2.2 Exemples
monter: 1.2 Applications différentiables
précédent: 1.2 Applications différentiables
Table des matières
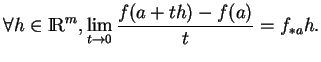
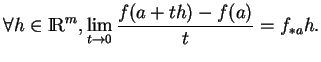
![]() les vecteurs
les vecteurs
![]() de la base canonique de
de la base canonique de
![]() , on voit que si
, on voit que si ![]() est différentiable en
est différentiable en ![]() , ses dérivées partielles
, ses dérivées partielles
![]() en
en ![]() existent. De plus,
existent. De plus, ![]() étant linéaire,
étant linéaire,
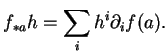
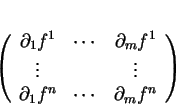
![]() est l'application linéaire tangente de
est l'application linéaire tangente de ![]() en
en ![]() , ou encore, un peu abusivement, la différentielle de
, ou encore, un peu abusivement, la différentielle de ![]() en
en ![]() .
Notons que
.
Notons que ![]() est la dérivée en
est la dérivée en ![]() de la fonction
de la fonction
d'une fonction
sont de classe
dans
, alors
est différentiable.