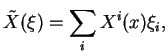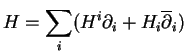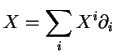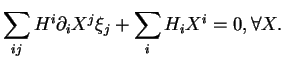Preuve.
Supposons que
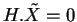
pour tout
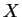
et montrons que
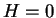
.
Notons
l'expression locale de
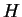
dans une carte canonique et
celle de
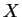
dans la carte à laquelle elle est associée.
On a donc
Fixons
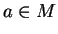
dans le domaine de cette carte. En prenant
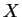
égal à
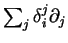
au voisinage de
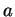
, on en déduit que
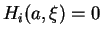
pour tout
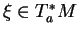
. En prenant ensuite
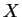
égal à
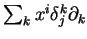
au voisinage de
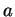
, il vient alors
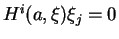
. Par conséquent,
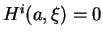
pour autant que
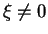
. On obtient
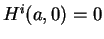
par continuité.
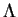
![]() . On note
. On note
![]() la fonction
la fonction