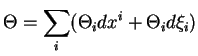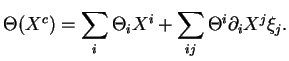Le relèvement complet ![]() d'un champ de vecteurs
d'un champ de vecteurs ![]() de
de ![]() est le champ de vecteurs de
est le champ de vecteurs de ![]() défini par
défini par
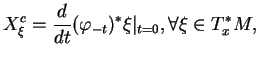
Dans une carte canonique, avec des notations familières, l'expression locale de ![]() s'écrit
s'écrit
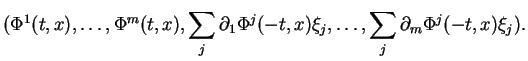
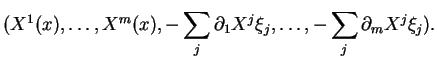
![\begin{displaymath}
% latex2html id marker 14383\begin{array}{rcl}
X^c_\xi.\ti...
...varphi(x)}\vert _{t=0}}})\\ [1ex]
&=&\xi([X,Y]_x).
\end{array}\end{displaymath}](img1044.gif)
On peut aussi vérifier la proposition précédente en calculant
![]() en coordonnées locales à l'aide des deux formules (12) et (13).
en coordonnées locales à l'aide des deux formules (12) et (13).
![\begin{displaymath}
% latex2html id marker 14412\begin{array}{rcl}
[X^c,Y^c].\...
...[[X,Y],Z]\ \tilde{ }\\ [1ex]
&=&[X,Y]^c.\tilde{Z}.
\end{array}\end{displaymath}](img1050.gif)