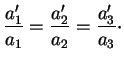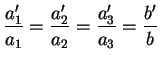suivant: 2.8 Le théorème de
monter: 2.7 Equations paramétriques et
précédent: 2.7.3 En dimension 2
Table des matières
On suppose maintenant que
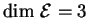 .
.
La droite passant par  de coordonnée
de coordonnée
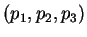 et de vecteur-directeur
et de vecteur-directeur 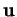 de composantes
de composantes
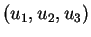 admet les équations cartésiennes
admet les équations cartésiennes
(ceci traduit de nouveau le fait que
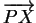 est un multiple de
est un multiple de 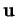 ).
).
La droite
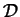 d'équations cartésiennes
d'équations cartésiennes
a pour sous-vectoriel directeur la droite vectorielle d'équations
)
Les vecteur-directeurs de
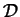 sont donc les vecteurs dont les composantes sont les multiples (non nuls) de (cf. Section 5.6)
sont donc les vecteurs dont les composantes sont les multiples (non nuls) de (cf. Section 5.6)
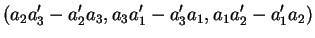 |
(2.6) |
formé des mineurs algébriques du tableau des coefficients des équations de
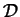 . Celle-ci est parallèle au plan d'équation
pour autant qu'un de ses vecteurs-directeurs ait des composantes solutions de l'équation homogène correspondante. Cette condition exprimée pour (14)
s'écrit
. Celle-ci est parallèle au plan d'équation
pour autant qu'un de ses vecteurs-directeurs ait des composantes solutions de l'équation homogène correspondante. Cette condition exprimée pour (14)
s'écrit
Proposition 2.7.2
Supposons que les plans

et
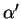
d'équations
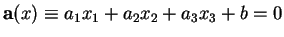
et
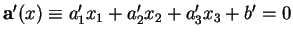
se coupent selon une droite
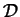
. Les plans contenant
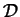
sont exactement les plans admettant une équation cartésienne de la forme
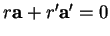
, où
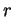
et
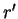
ne sont pas tous les deux nuls.
Preuve. Soit un plan 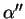 d'équation cartésienne
d'équation cartésienne
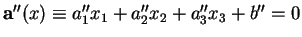 contenant
contenant
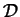 . Puisque
. Puisque
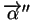 contient
contient
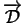 , il résulte de la Proposition 5.13 qu'il existe des nombres non tous nuls
, il résulte de la Proposition 5.13 qu'il existe des nombres non tous nuls 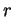 et
et 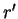 tels que
En exprimant que
tels que
En exprimant que 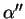 passe par un point de
passe par un point de
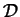 , on vérifie comme dans la preuve de la Proposition 7.1 que
, on vérifie comme dans la preuve de la Proposition 7.1 que
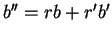 .
.
Corollaire 2.7.3
Le plan passant par la droite
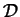
d'équations cartésiennes
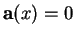
,
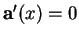
et par le point

non situé sur
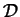
de coordonnée
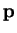
admet l'équation cartésienne
Le plan passant par le point  de coordonnée
de coordonnée
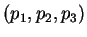 et admettant les vecteurs directeurs linéairement indépendants
et admettant les vecteurs directeurs linéairement indépendants 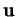 et
et 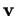 de composantes
de composantes
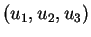 et
et
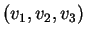 admet l'équation cartésienne
admet l'équation cartésienne
qui exprime que
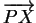 est combinaison linéaire de
est combinaison linéaire de 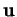 et
et 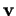 . D'ailleurs, c'est manifestement une équation du premier degré et les propriétés des
déterminants vis-à-vis des colonnes montrent qu'elle est vérifiée lorsque
. D'ailleurs, c'est manifestement une équation du premier degré et les propriétés des
déterminants vis-à-vis des colonnes montrent qu'elle est vérifiée lorsque
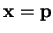 et que l'équation homogène l'est par les composantes de
et que l'équation homogène l'est par les composantes de 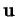 et de
et de 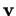 .
Elle s'écrit aussi
.
Elle s'écrit aussi
Le plan passant par trois points non alignés  ,
, 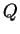 ,
, 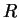 de coordonnées
de coordonnées
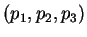 ,
,
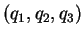 et
et
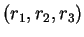 a dès lors pour équation
a dès lors pour équation
que l'on écrit aussi sous la forme équivalente
Le sous-vectoriel directeur du plan  d'équation cartésienne
d'équation cartésienne
ayant pour équation
le plan 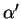 d'équation
est parallèle à
d'équation
est parallèle à  si et seulement si (cf. Section 5.6)
Il coïncide alors avec
si et seulement si (cf. Section 5.6)
Il coïncide alors avec  si
(la vérification est la même qu'à propos du parallélisme de droites dans un plan).
si
(la vérification est la même qu'à propos du parallélisme de droites dans un plan).




suivant: 2.8 Le théorème de
monter: 2.7 Equations paramétriques et
précédent: 2.7.3 En dimension 2
Table des matières
2002-12-17
![]() .
.
![]() de coordonnée
de coordonnée
![]() et de vecteur-directeur
et de vecteur-directeur ![]() de composantes
de composantes
![]() admet les équations cartésiennes
admet les équations cartésiennes
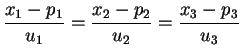
![]() d'équations cartésiennes
d'équations cartésiennes
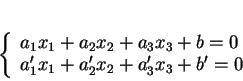
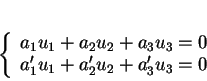
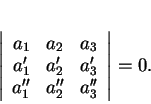
![]() de coordonnée
de coordonnée
![]() et admettant les vecteurs directeurs linéairement indépendants
et admettant les vecteurs directeurs linéairement indépendants ![]() et
et ![]() de composantes
de composantes
![]() et
et
![]() admet l'équation cartésienne
admet l'équation cartésienne
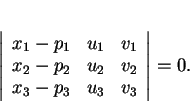
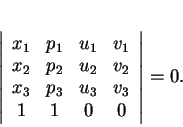
![]() ,
, ![]() ,
, ![]() de coordonnées
de coordonnées
![]() ,
,
![]() et
et
![]() a dès lors pour équation
a dès lors pour équation
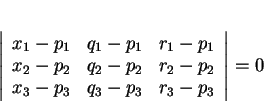
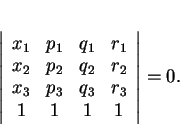
![]() d'équation cartésienne
d'équation cartésienne