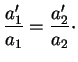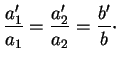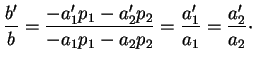Supposons que
![]() .
.
La droite passant par ![]() de coordonnée
de coordonnée ![]() et de vecteur-directeur
et de vecteur-directeur ![]() de composantes
de composantes ![]() admet l'équation cartésienne
admet l'équation cartésienne
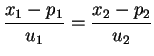
La droite passant par des points distincts ![]() et
et ![]() de coordonnées
de coordonnées ![]() et
et ![]() admet l'équation cartésienne
admet l'équation cartésienne
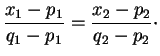
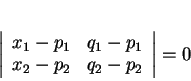
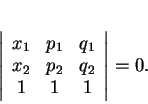
Le sous-vectoriel directeur de la droite
![]() d'équation cartésienne
d'équation cartésienne