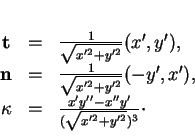suivant: 6.4.2 Equation cartésienne
monter: 6.4 Courbes planes
précédent: 6.4 Courbes planes
Table des matières
Rapportons
 à un repère orthonormé, ce qui a pour effet de nous ramener dans
à un repère orthonormé, ce qui a pour effet de nous ramener dans
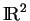 muni du produit scalaire canonique. Pour alléger l'écriture,
dans le reste de cette section, on explicite directement les formules en coordonnées.
muni du produit scalaire canonique. Pour alléger l'écriture,
dans le reste de cette section, on explicite directement les formules en coordonnées.
Une manière commode de se donner une courbe consiste à la décrire comme un graphe de fonction. Le graphe
de la fonction
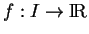 de classe
de classe 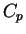 est un arc paramétré de courbe de classe
est un arc paramétré de courbe de classe 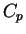 . Il admet en effet le paramétrage distingué
. Il admet en effet le paramétrage distingué
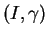 , où
est injectif. Comme
, où
est injectif. Comme 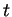 est l'abscisse de
est l'abscisse de 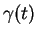 , on dit que c'est le paramétrage par l'abscisse de
, on dit que c'est le paramétrage par l'abscisse de 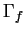 .
.
Proposition 6.4.2
Soit une fonction
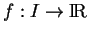
de classe
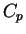
. Si
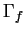
est orienté par le paramétrage par l'abscisse, alors sa tangente unitaire,
sa normale principale et sa courbure sont respectivement donnés par
Preuve. La formule pour 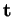 résulte immédiatement de la définition du paramétrage par l'abscisse.
La normale
résulte immédiatement de la définition du paramétrage par l'abscisse.
La normale 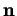 est alors nécessairement l'un des vecteurs
Pour lever l'ambiguïté sur le signe, il suffit d'observer que
Après un peu de calcul, on obtient alors
ce qui donne directement l'expression prévue pour la courbure.
est alors nécessairement l'un des vecteurs
Pour lever l'ambiguïté sur le signe, il suffit d'observer que
Après un peu de calcul, on obtient alors
ce qui donne directement l'expression prévue pour la courbure.
Le signe de 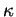 est celui de
est celui de 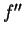 . Il est donc lié à la concavité
de
. Il est donc lié à la concavité
de 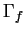 : la concavité est ``vers le haut" ou ``vers le
bas" selon que
: la concavité est ``vers le haut" ou ``vers le
bas" selon que 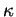 est positif ou négatif. Plus intrinsèquement, cela
signifie que
est positif ou négatif. Plus intrinsèquement, cela
signifie que 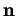 est orienté vers la concavité ou l'opposé de
est orienté vers la concavité ou l'opposé de 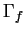 selon que
selon que 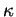 est positif ou négatif.
est positif ou négatif.
On peut également considérer des arcs paramétrés par l'ordonnée, en échangeant ci-dessus les rôles des coordonnées 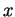 et de
et de 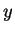 .
.
On peut aussi exprimer
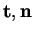 et
et 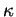 lorsque l'arc est orienté par un paramétrage quelconque
lorsque l'arc est orienté par un paramétrage quelconque
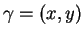 .
On obtient alors
.
On obtient alors




suivant: 6.4.2 Equation cartésienne
monter: 6.4 Courbes planes
précédent: 6.4 Courbes planes
Table des matières
2002-12-17
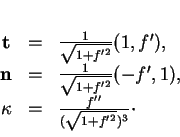
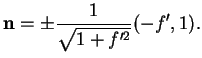
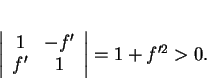
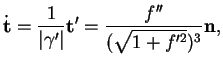
![]() est celui de
est celui de ![]() . Il est donc lié à la concavité
de
. Il est donc lié à la concavité
de ![]() : la concavité est ``vers le haut" ou ``vers le
bas" selon que
: la concavité est ``vers le haut" ou ``vers le
bas" selon que ![]() est positif ou négatif. Plus intrinsèquement, cela
signifie que
est positif ou négatif. Plus intrinsèquement, cela
signifie que ![]() est orienté vers la concavité ou l'opposé de
est orienté vers la concavité ou l'opposé de ![]() selon que
selon que ![]() est positif ou négatif.
est positif ou négatif.
![]() et de
et de ![]() .
.
![]() et
et ![]() lorsque l'arc est orienté par un paramétrage quelconque
lorsque l'arc est orienté par un paramétrage quelconque
![]() .
On obtient alors
.
On obtient alors