

suivant: 0.3.1 Le lemme de
monter: Quelques remarques sur les
précédent: 0.2.5 Premiers et derniers
Nous allons illustrer certaines questions de la sous-section ![[*]](crossref.gif) lorsque le système
lorsque le système 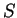 est le système de numération de position associé à une base
est le système de numération de position associé à une base 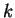 en présentant quelques propriétés élémentaires des ensembles d'entiers
en présentant quelques propriétés élémentaires des ensembles d'entiers 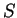 -reconnaissables. Nous remplacerons les notations
-reconnaissables. Nous remplacerons les notations 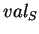 et
et 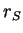 par
par 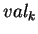 et
et 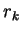 respectivement et nous utiliserons ``
respectivement et nous utiliserons ``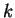 -reconnaissable'' à la place de ``
-reconnaissable'' à la place de ``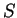 -reconnaissable''.
-reconnaissable''.
La numération en base 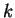 possède une propriété importante. Supposons que
possède une propriété importante. Supposons que 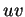 soit un mot du langage (
soit un mot du langage (![[*]](crossref.gif) ) de la numération. Le mot
) de la numération. Le mot 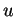 appartient toujours à ce langage car il ne commence pas par 0. Si
appartient toujours à ce langage car il ne commence pas par 0. Si 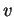 ne commence pas par 0 non plus, alors il appartient aussi à (
ne commence pas par 0 non plus, alors il appartient aussi à (![[*]](crossref.gif) ) et
) et
Si 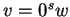 où
où 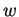 appartient à (
appartient à (![[*]](crossref.gif) ),
), 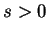 , il faut remplacer
, il faut remplacer 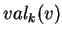 par
par 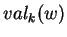 dans cette formule. On peut uniformiser celle-ci en convenant d'étendre
dans cette formule. On peut uniformiser celle-ci en convenant d'étendre 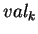 en posant dans ce cas
en posant dans ce cas
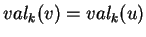 , ce que nous ferons désormais. Par exemple,
, ce que nous ferons désormais. Par exemple,
Dans la suite de cette section, nous considérons une partie
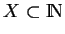 . Nous rangeons ses éléments par ordre croissant:
. Nous rangeons ses éléments par ordre croissant:
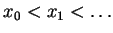
Sous-sections


suivant: 0.3.1 Le lemme de
monter: Quelques remarques sur les
précédent: 0.2.5 Premiers et derniers
2002-12-17
![[*]](crossref.gif) lorsque le système
lorsque le système ![]() possède une propriété importante. Supposons que
possède une propriété importante. Supposons que ![]() soit un mot du langage (
soit un mot du langage (![[*]](crossref.gif) ) de la numération. Le mot
) de la numération. Le mot ![]() appartient toujours à ce langage car il ne commence pas par 0. Si
appartient toujours à ce langage car il ne commence pas par 0. Si ![]() ne commence pas par 0 non plus, alors il appartient aussi à (
ne commence pas par 0 non plus, alors il appartient aussi à (![[*]](crossref.gif) ) et
) et
![[*]](crossref.gif) ),
), ![\begin{displaymath}
% latex2html id marker 3286\begin{array}{rllll}
val_{10}(1...
...}(41)\\ [1ex]
&=&val_{10}(12)10^3&+&val_{10}(041).
\end{array}\end{displaymath}](img272.gif)
![]() . Nous rangeons ses éléments par ordre croissant:
. Nous rangeons ses éléments par ordre croissant:
![]()