



suivant: 6.1.3 Calcul des longueurs
monter: 6.1 La première forme
précédent: 6.1.1 Définition
Table des matières
La préoccupation est ici la
même que celle qui a conduit au formules de Frenet pour les courbes.
Il s'agit de dériver
les éléments décrivant localement espace tangent et normale. Nous
reviendrons ultérieurement plus en détail sur la normale. Ici, nous
notons 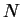 une
fonction qui associe à chaque point
une
fonction qui associe à chaque point 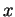 de
de  un élément
un élément
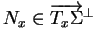 . Nous supposons qu'exprimée à l'aide
du paramétrage
. Nous supposons qu'exprimée à l'aide
du paramétrage  ,
elle est dérivable en
,
elle est dérivable en 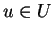 autant de fois que nécessaire.
autant de fois que nécessaire.
Proposition 37
Il existe des fonctions
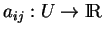
telles que
pour tous
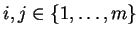
, où les coefficients
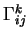
sont déterminés par
Nous pouvons de fait décomposer
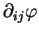 selon la
base
selon la
base
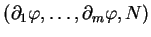 de
de
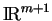 .
Nous laissons de côté les coefficients
.
Nous laissons de côté les coefficients 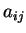 de
de 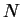 . Pour calculer
le coefficient
. Pour calculer
le coefficient
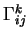 de
de
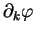 , on évalue
Remarquons préalablement que
En permutant circulairement les indices
, on évalue
Remarquons préalablement que
En permutant circulairement les indices 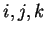 puis en additionnant
les égalités obtenues membre à membre, il vient
La proposition en résulte immédiatement.
puis en additionnant
les égalités obtenues membre à membre, il vient
La proposition en résulte immédiatement.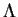
Remarquons que les symboles de Christoffel
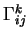 sont
des fonctions de classe
sont
des fonctions de classe 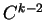 . Il en va dès lors de même pour les
composantes
. Il en va dès lors de même pour les
composantes 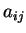 pourvu que
pourvu que 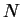 soit aussi de cette classe. Nous verrons qu'il peut
être supposé de classe
soit aussi de cette classe. Nous verrons qu'il peut
être supposé de classe 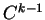 .
.
Les symboles de Christoffel d'un cylindre
circulaire droit paramétré par
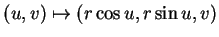 sont
nuls. A titre d'exercice, le lecteur déterminera les coefficient de Christoffel pour la sphère
paramétrée par
sont
nuls. A titre d'exercice, le lecteur déterminera les coefficient de Christoffel pour la sphère
paramétrée par
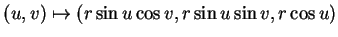 .
.




suivant: 6.1.3 Calcul des longueurs
monter: 6.1 La première forme
précédent: 6.1.1 Définition
Table des matières
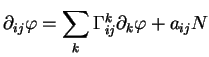
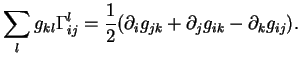
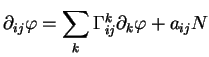
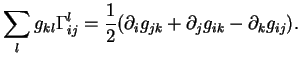
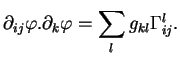
![]() sont
des fonctions de classe
sont
des fonctions de classe ![]() . Il en va dès lors de même pour les
composantes
. Il en va dès lors de même pour les
composantes ![]() pourvu que
pourvu que ![]() soit aussi de cette classe. Nous verrons qu'il peut
être supposé de classe
soit aussi de cette classe. Nous verrons qu'il peut
être supposé de classe ![]() .
.
![]() sont
nuls. A titre d'exercice, le lecteur déterminera les coefficient de Christoffel pour la sphère
paramétrée par
sont
nuls. A titre d'exercice, le lecteur déterminera les coefficient de Christoffel pour la sphère
paramétrée par
![]() .
.