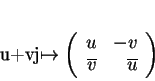


suivant: 4.3.3 et l'espace projectif
monter: 4.3 La sphère ,
précédent: 4.3.1.2 Les plongements de
Table des matières
On note encore
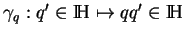 la multiplication à gauche par
le quaternion
la multiplication à gauche par
le quaternion
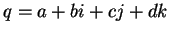 . C'est
une application linéaire réelle. Dans la base
. C'est
une application linéaire réelle. Dans la base
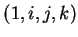 , elle est représentée par la matrice (avec laquelle on la
confond dans la suite)
, elle est représentée par la matrice (avec laquelle on la
confond dans la suite)
La multiplication des quaternions étant associative, on a
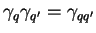 . Les nombres réels correspondent
aux multiples de l'identité:
si
. Les nombres réels correspondent
aux multiples de l'identité:
si
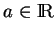 , alors
, alors
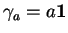 . De plus, le conjugé d'un quaternion
. De plus, le conjugé d'un quaternion 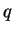 est représenté par la matrice
est représenté par la matrice
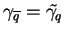 . En particulier,
. En particulier,
Lemme 18
Soit un quaternion
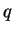
. On a
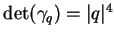
.
Si
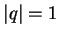
,
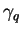
est une matrice de rotation: c'est un élément
de
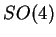
.
Naturellement, le calcul de
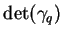 peut se faire de
façon directe en développant le déterminant de la matrice
peut se faire de
façon directe en développant le déterminant de la matrice 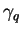 .
Voici une manière de faire plus rapide. En prenant le déterminant des deux
membres de
.
Voici une manière de faire plus rapide. En prenant le déterminant des deux
membres de
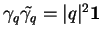 , on obtient
, on obtient
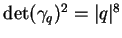 , donc
, donc
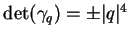 . Mais
. Mais
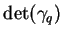 et
et
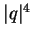 sont deux polynômes dont les termes en
sont deux polynômes dont les termes en 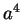 sont égaux.
sont égaux.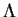
Lemme 19
Pour tous quaternions
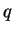
et
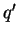
, on a
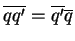
et
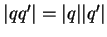
.
On a en effet
Par conséquent,
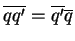 . De plus
. De plus
D'où la conclusion puisque les modules sont positifs ou nuls.
Proposition 20
La sphère
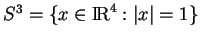
, ensemble des quaternions de
module
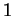
, est un groupe pour la multiplication des
quaternions, sous-groupe de
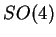
.
C'est un corollaire immédiat des lemmes qui précèdent.
L'écriture des quaternions à l'aide de nombres complexes donne une
autre interprétation de la strucutre de groupe de 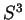 .
.
Proposition 21
L'application
est un isomorphismes de groupes entre
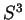
et
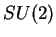
.
Les lignes d'une matrice unitaire sont orthogonales et normées
(au sens du produit scalaire de
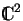 ). Si la première peut
s'écrire, arbitrairement,
). Si la première peut
s'écrire, arbitrairement, 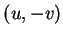 , où
, où
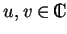 sont tels que
sont tels que
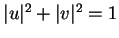 , la seconde est
alors un multiple de
, la seconde est
alors un multiple de
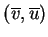 . Pour que le
déterminant de la matrice soit
. Pour que le
déterminant de la matrice soit
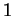 , il faut que ce multiple soit
, il faut que ce multiple soit 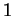 . La correspondance indiquée est
donc une bijection entre
. La correspondance indiquée est
donc une bijection entre 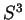 et
et 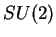 .
Le fait que cela soit un homomorphisme de groupes résulte aisément de (6).
.
Le fait que cela soit un homomorphisme de groupes résulte aisément de (6).



suivant: 4.3.3 et l'espace projectif
monter: 4.3 La sphère ,
précédent: 4.3.1.2 Les plongements de
Table des matières
![]() la multiplication à gauche par
le quaternion
la multiplication à gauche par
le quaternion
![]() . C'est
une application linéaire réelle. Dans la base
. C'est
une application linéaire réelle. Dans la base
![]() , elle est représentée par la matrice (avec laquelle on la
confond dans la suite)
, elle est représentée par la matrice (avec laquelle on la
confond dans la suite)
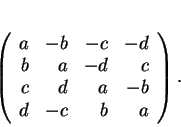
![]() .
.