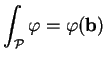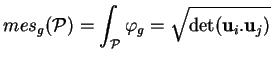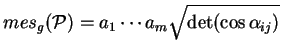suivant: A..6.3 Cas des espaces
monter: A..6 Densités et intégration
précédent: A..6.1 Cas d'un espace
Table des matières
Soit un parallélotope
de
 . Les éléments
. Les éléments 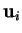 de
de  forment une base
forment une base 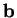 de
de  et les coordonnées des points de
et les coordonnées des points de
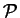 dans le repère
dans le repère
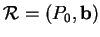 décrivent exactement le cube
décrivent exactement le cube ![$ [0,1]^m$](img1962.gif) de
de
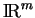 . Par conséquent, pour toute densité
. Par conséquent, pour toute densité  de poids
de poids  de
de  , le champ de
, le champ de  -densités constant
-densités constant
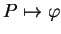 de
de
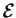 (nous le notons encore
(nous le notons encore  ) est intégrable sur
) est intégrable sur
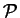 et
En particulier, lorsque
et
En particulier, lorsque  est la densité
est la densité 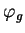 canoniquement asociée à un produit scalaire
canoniquement asociée à un produit scalaire
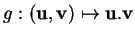 de
de  , la formule (23) montre que la mesure de
, la formule (23) montre que la mesure de
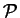 est donnée par
Dans ce déterminant, on voit apparaître
est donnée par
Dans ce déterminant, on voit apparaître
- les côtés issus du sommet
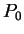 :
:
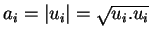
- les angles que font ces côtés, donnés par
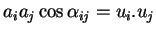
On peut ainsi écrire
En particulier, si tous les 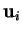 sont deux à deux perpendiculaires, on obtient
sont deux à deux perpendiculaires, on obtient




suivant: A..6.3 Cas des espaces
monter: A..6 Densités et intégration
précédent: A..6.1 Cas d'un espace
Table des matières