



suivant: A..5.2 Exemples
monter: A..5 Densités et produits
précédent: A..5 Densités et produits
Table des matières
Nous atteignons enfin un de nos objectifs, à savoir montrer que tout produit scalaire induit naturellement une densité de poids donné sur  . Ceci est lié à l'existence de l'application
. Ceci est lié à l'existence de l'application 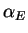 .
.
Soit un produit scalaire 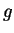 sur
sur  . On pose
. On pose
où, pour rappel, 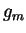 désigne le produit scalaire canonique de
désigne le produit scalaire canonique de
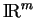 . On obtient ainsi une
. On obtient ainsi une 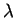 -densité sur
-densité sur  , comme le montre immédiatement la formule b) de la proposition
, comme le montre immédiatement la formule b) de la proposition ![[*]](crossref.gif) .
.
Si 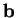 est ue base orthonormée pour
est ue base orthonormée pour 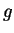 , alors
, alors
ce qui caractérise
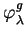 vu la propsoition 70. En général, on peut calculer
vu la propsoition 70. En général, on peut calculer
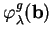 à l'aide de la matrice
formée des composantes
à l'aide de la matrice
formée des composantes 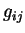 de
de 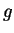 dans la base
dans la base 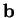 .
.
Proposition 74
On a
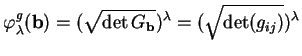 |
(A.3) |
En effet, si 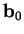 est une base orthonormée pour
est une base orthonormée pour 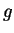 et si
et si
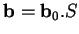 , alors
De là
, alors
De là
La densité
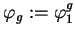 de poids
de poids  est positive et
est positive et
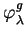 s'obtient en l'élevant à la puissance
s'obtient en l'élevant à la puissance 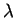 . De plus, le produit scalaire
. De plus, le produit scalaire 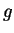 de
de  induit par restriction un produit scalaire
induit par restriction un produit scalaire 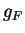 sur chaque sous-espace vectoriel de
sur chaque sous-espace vectoriel de  . Il fournit donc automatiquement une base de chaque espace
. Il fournit donc automatiquement une base de chaque espace
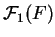 .
.




suivant: A..5.2 Exemples
monter: A..5 Densités et produits
précédent: A..5 Densités et produits
Table des matières
![]() sur
sur ![]() . On pose
. On pose
![[*]](crossref.gif) .
.
![]() est ue base orthonormée pour
est ue base orthonormée pour ![]() , alors
, alors
![]() de poids
de poids ![]() est positive et
est positive et
![]() s'obtient en l'élevant à la puissance
s'obtient en l'élevant à la puissance ![]() . De plus, le produit scalaire
. De plus, le produit scalaire ![]() de
de ![]() induit par restriction un produit scalaire
induit par restriction un produit scalaire ![]() sur chaque sous-espace vectoriel de
sur chaque sous-espace vectoriel de ![]() . Il fournit donc automatiquement une base de chaque espace
. Il fournit donc automatiquement une base de chaque espace
![]() .
.