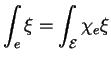suivant: A..6.2 Mesure des parallélotopes
monter: A..6 Densités et intégration
précédent: A..6 Densités et intégration
Table des matières
Soit un espace affine
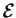 modelé sur
modelé sur  . Par définition, un champs de
. Par définition, un champs de  -densités (pour abréger, on dira encore une
-densités (pour abréger, on dira encore une  -densité) sur
-densité) sur
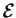 est une application
est une application
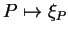 de
de
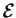 dans
dans
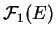 . Si nécessaire, nous noterons
. Si nécessaire, nous noterons
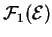 l'espace des champs de
l'espace des champs de  -densités de
-densités de
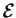 .
.
Dans un repère
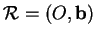 de
de
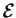 , d'origine
, d'origine
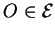 et de base
et de base
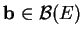 , un champs de
, un champs de  -densités
-densités 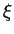 est comlètement décrit par la fonction
est comlètement décrit par la fonction
où, par commodité, nous avons désigné par
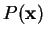 le point
le point
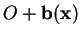 de coordonnées
de coordonnées 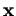 dans ce repère. Cette fonction n'est autre que la fonction
dans ce repère. Cette fonction n'est autre que la fonction
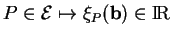 exprimée au moyen des coordonénes cartésiennes définies par
exprimée au moyen des coordonénes cartésiennes définies par
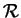 .
.
Lemme 75
Soit un champ de

-densités
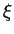
de
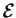
.
Les expressions
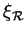
et
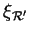
de
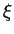
dans des repères
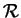
et
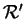
de
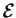
sont simultanément intégrables ou non sur
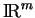
et, quand elles le sont, leurs intégrales sont égales.
Notons 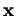 et
et 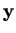 les coordonnées cartésiennes d'un point
les coordonnées cartésiennes d'un point 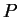 relatives aux repères
relatives aux repères
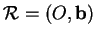 et
et
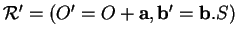 respectivement. On doit avoir
En conséquence,
Dès lors
La conclusion résulte alors immédiatement du théorème de changement de variables dans les intégrales.
respectivement. On doit avoir
En conséquence,
Dès lors
La conclusion résulte alors immédiatement du théorème de changement de variables dans les intégrales.
Grâce à ce lemme, nous pouvons dire que
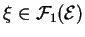 est intégrable si son expression
est intégrable si son expression
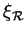 dans un certain repère
dans un certain repère
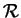 (donc dans tous les repères) de
(donc dans tous les repères) de
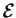 est intégrable sur
est intégrable sur
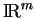 et, quand c'est le cas, nous pouvons aussi définir l'intégrale de
et, quand c'est le cas, nous pouvons aussi définir l'intégrale de 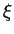 comme étant le nombre
comme étant le nombre
Comme dans
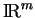 , on peut aussi introduire la notion de densité intégrable sur un ensemble
, on peut aussi introduire la notion de densité intégrable sur un ensemble
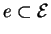 et définir les intégrales d'un champs de densités
et définir les intégrales d'un champs de densités 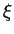 sur
sur  . Par définition, c'est l'intégrale de la
. Par définition, c'est l'intégrale de la  -densité
-densité 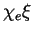 , où
, où 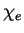 est la fonction caractéristique de
est la fonction caractéristique de  ,
,
si elle existe.




suivant: A..6.2 Mesure des parallélotopes
monter: A..6 Densités et intégration
précédent: A..6 Densités et intégration
Table des matières
![]() de
de
![]() , d'origine
, d'origine
![]() et de base
et de base
![]() , un champs de
, un champs de ![]() -densités
-densités ![]() est comlètement décrit par la fonction
est comlètement décrit par la fonction
![]() est intégrable si son expression
est intégrable si son expression
![]() dans un certain repère
dans un certain repère
![]() (donc dans tous les repères) de
(donc dans tous les repères) de
![]() est intégrable sur
est intégrable sur
![]() et, quand c'est le cas, nous pouvons aussi définir l'intégrale de
et, quand c'est le cas, nous pouvons aussi définir l'intégrale de ![]() comme étant le nombre
comme étant le nombre
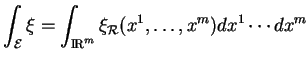
![]() , on peut aussi introduire la notion de densité intégrable sur un ensemble
, on peut aussi introduire la notion de densité intégrable sur un ensemble
![]() et définir les intégrales d'un champs de densités
et définir les intégrales d'un champs de densités ![]() sur
sur ![]() . Par définition, c'est l'intégrale de la
. Par définition, c'est l'intégrale de la ![]() -densité
-densité ![]() , où
, où ![]() est la fonction caractéristique de
est la fonction caractéristique de ![]() ,
,