



suivant: A..6.4 Cas des variétés
monter: A..6 Densités et intégration
précédent: A..6.2 Mesure des parallélotopes
Table des matières
Lorsque  est muni d'un produit scalaire,
est muni d'un produit scalaire,
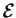 est un espace affine euclidien. Il est automatiquement muni d'un champ de
est un espace affine euclidien. Il est automatiquement muni d'un champ de  -densités, le champ de valeur constante
-densités, le champ de valeur constante 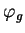 dont il vient d'être question. Comme ce dernier fournit une base des densités de
dont il vient d'être question. Comme ce dernier fournit une base des densités de  , les
, les  -densités sur
-densités sur
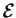 sont exactement les applications de la forme
où
sont exactement les applications de la forme
où  décrit l'ensemble des fonctions de
décrit l'ensemble des fonctions de
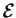 dans
dans
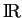 . Puisque, sur les bases orthonormées,
. Puisque, sur les bases orthonormées, 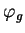 prend la valeur
prend la valeur  , l'expression de
, l'expression de 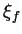 dans un repère orthonormé
dans un repère orthonormé
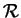 de
de
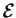 coïncide avec l'expression
de
coïncide avec l'expression
de  dans ce repère. On est ainsi amené à confondre les fonctions sur
dans ce repère. On est ainsi amené à confondre les fonctions sur
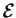 avec ses
avec ses  -densités et à parler de fonctions intégrables et de leurs intégrales. Il ne faut cependant pas perdre de vue que les fonctions, comme telles, ne peuvent pas être intégrées sur
-densités et à parler de fonctions intégrables et de leurs intégrales. Il ne faut cependant pas perdre de vue que les fonctions, comme telles, ne peuvent pas être intégrées sur
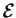 : lors d'un changement de repères arbitraires, leurs expressions ne se comportent pas en accord avec le théorème de changement de variables dans les intégrales.
: lors d'un changement de repères arbitraires, leurs expressions ne se comportent pas en accord avec le théorème de changement de variables dans les intégrales.




suivant: A..6.4 Cas des variétés
monter: A..6 Densités et intégration
précédent: A..6.2 Mesure des parallélotopes
Table des matières