



suivant: 4.5 Longueurs, aires et
monter: 4.4 Distance
précédent: 4.4.3.1 Coordonnées polaires et
Table des matières
Les formules d'Appolonius expriment la moyenne des carrés des distances d'un point à des points donnés au moyen des distances de chacun à leur barycentre.
Lorsque la somme des poids est nulle, une identité analogue met en jeu le vecteur représenté par la moyenne pondérée de ces points.
Divers résultats en découlent parmi lesquels de nombreux lieux géométriques.
Proposition 4.4.9
(Formules d'Appolonius) Soient des points
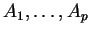
et des poids
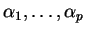
.
(i) Si
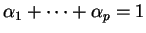 , alors pour tout point
, alors pour tout point 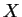 ,
,
où
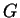
est le barycentre
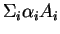
.
(ii) Si
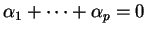 , alors pour tous
, alors pour tous 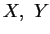 ,
,
où
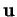
est le vecteur
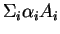
.
Preuve. On a
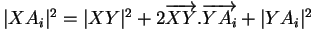 . On multiplie cette relation par
. On multiplie cette relation par 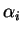 puis on additionne membre à membre les égalités ainsi
obtenues lorsque
puis on additionne membre à membre les égalités ainsi
obtenues lorsque 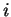 varie de
varie de 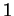 à
à 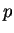 . Cela donne immédiatement (ii) quand la somme des
. Cela donne immédiatement (ii) quand la somme des 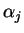 est nulle. Quand elle vaut
est nulle. Quand elle vaut 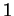 , cela donne (i) pour autant
qu'on prenne
, cela donne (i) pour autant
qu'on prenne 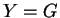 .
. 
Le corollaire suivant est facile à obtenir. Il est laissé comme exercice.
Corollaire 4.4.10
Soient des points
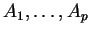
, des poids
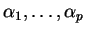
et
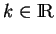
.
Si
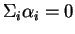
et si
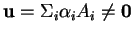
, alors l'ensemble des points
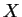
pour lesquels
est un hyperplan admettant de normale
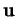
. Si
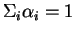
et
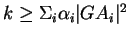
,
c'est la sphère de centre
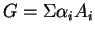
et de rayon
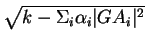
.
Il est vide quand
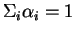
et
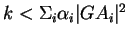
.
Exemple 4.4.11
L'hyperplan médiateur
Le corollaire appliqué à deux points, avec les poids 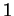 et
et 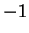 , montre que l'ensemble des points équidistants de deux points est l'hyperplan
passant par le milieu du segment délimité par ces points et perpendiculaire à la droite qu'ils déterminent. On l'appelle l'hyperplan médiateur des deux points.
, montre que l'ensemble des points équidistants de deux points est l'hyperplan
passant par le milieu du segment délimité par ces points et perpendiculaire à la droite qu'ils déterminent. On l'appelle l'hyperplan médiateur des deux points.
Exemple 4.4.12
Le théorème de la médiane
D'après le corollaire appliqué avec les deux poids 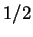 et
et 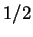 , les points
, les points 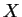 d'un plan dont la somme des carrés des distances à deux points
d'un plan dont la somme des carrés des distances à deux points 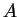 et
et 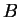 est
constante est vide ou est un cercle dont le centre est le milieu
est
constante est vide ou est un cercle dont le centre est le milieu 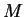 du segment joignant
du segment joignant 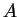 et
et 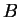 . Si
. Si 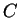 forme un triangle avec
forme un triangle avec 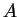 et
et 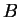 , on a donc, puisque
, on a donc, puisque
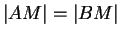 ,
,
C'est le théorème de la médiane.
Proposition 4.4.13
Si
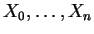
forment un simplexe, alors il appartiennent à une sphère.
Preuve. L'existence de la sphère se démontre par récurrence sur la dimension 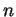 de
de
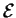 .
Pour
.
Pour 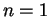 , c'est immédiat, la sphère étant alors réduite aux deux points
, c'est immédiat, la sphère étant alors réduite aux deux points 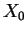 et
et 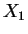 , son centre étant le milieu du segment qui les joint.
Passons alors "de
, son centre étant le milieu du segment qui les joint.
Passons alors "de 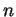 à
à 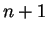 ". Considérons un simplexe
". Considérons un simplexe
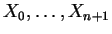 et notons
et notons 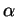 l'hyperplan contenant
l'hyperplan contenant
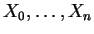 .
Par hypothèse de récurrence, ceux-ci appartiennent à une sphère de
.
Par hypothèse de récurrence, ceux-ci appartiennent à une sphère de 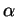 . Notons
. Notons 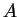 son centre.
son centre.
Nous allons voir que l'on peut choisir un point équidistant des 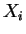 ,
,
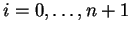 , sur la perpendiculaire
, sur la perpendiculaire
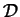 à
à 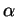 passant par
passant par 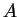 .
.
Remarquons d'abord que les points de
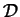 sont équidistants de
sont équidistants de
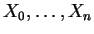 . En effet, si
. En effet, si
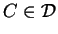 et
et 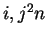 , alors
, alors
car d'une part, les produits scalaires
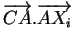 et
et
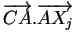 sont nuls puisque
sont nuls puisque 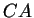 est orthogonal à
est orthogonal à 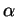 et d'autre part,
et d'autre part,
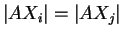 puisque
puisque 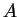 est le centre d'une sphère contenant
est le centre d'une sphère contenant 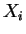 et
et 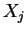 .
.
La droite
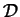 perce le plan médiateur de
perce le plan médiateur de 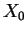 et
et 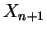 sinon
sinon
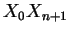 serait parallèle à
serait parallèle à 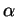 et
et 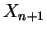 ne formerait pas un simplexe avec
les autres
ne formerait pas un simplexe avec
les autres 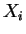 . Le point de percée de
. Le point de percée de
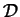 dans ce plan médiateur est équidistant de
dans ce plan médiateur est équidistant de 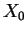 et
et 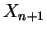 mais aussi, vu ce qui précède, des autres
mais aussi, vu ce qui précède, des autres 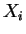 .
C'est donc le centre d'une sphère contenant tous les
.
C'est donc le centre d'une sphère contenant tous les 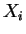 .
.
Remarque 4.4.14
Il existe au plus une seule sphère contenant des points formant un simplexe. Cela est aisé à vérifier.




suivant: 4.5 Longueurs, aires et
monter: 4.4 Distance
précédent: 4.4.3.1 Coordonnées polaires et
Table des matières
2002-12-17
![]() , alors pour tout point
, alors pour tout point ![]() ,
,
![]() , alors pour tous
, alors pour tous ![]() ,
,
![]() , alors pour tout point
, alors pour tout point ![]() ,
,
![]() , alors pour tous
, alors pour tous ![]() ,
,
![]() et
et ![]() , montre que l'ensemble des points équidistants de deux points est l'hyperplan
passant par le milieu du segment délimité par ces points et perpendiculaire à la droite qu'ils déterminent. On l'appelle l'hyperplan médiateur des deux points.
, montre que l'ensemble des points équidistants de deux points est l'hyperplan
passant par le milieu du segment délimité par ces points et perpendiculaire à la droite qu'ils déterminent. On l'appelle l'hyperplan médiateur des deux points.
![]() et
et ![]() , les points
, les points ![]() d'un plan dont la somme des carrés des distances à deux points
d'un plan dont la somme des carrés des distances à deux points ![]() et
et ![]() est
constante est vide ou est un cercle dont le centre est le milieu
est
constante est vide ou est un cercle dont le centre est le milieu ![]() du segment joignant
du segment joignant ![]() et
et ![]() . Si
. Si ![]() forme un triangle avec
forme un triangle avec ![]() et
et ![]() , on a donc, puisque
, on a donc, puisque
![]() ,
,
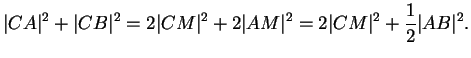
![]() ,
,
![]() , sur la perpendiculaire
, sur la perpendiculaire
![]() à
à ![]() passant par
passant par ![]() .
.
![]() sont équidistants de
sont équidistants de
![]() . En effet, si
. En effet, si
![]() et
et ![]() , alors
, alors
![]() perce le plan médiateur de
perce le plan médiateur de ![]() et
et ![]() sinon
sinon
![]() serait parallèle à
serait parallèle à ![]() et
et ![]() ne formerait pas un simplexe avec
les autres
ne formerait pas un simplexe avec
les autres ![]() . Le point de percée de
. Le point de percée de
![]() dans ce plan médiateur est équidistant de
dans ce plan médiateur est équidistant de ![]() et
et ![]() mais aussi, vu ce qui précède, des autres
mais aussi, vu ce qui précède, des autres ![]() .
C'est donc le centre d'une sphère contenant tous les
.
C'est donc le centre d'une sphère contenant tous les ![]() .
.![]()