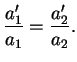suivant: 1.5.6 Cas de la
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.4.1 Les hyperplans vectoriels
Table des matières
1.5.5 Cas de la dimension 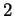
Lorsque  est de dimension
est de dimension 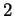 , les seuls sous-espaces vectoriels propres sont les droites vectorielles. Ce sont aussi des hyperplans vectoriels.
, les seuls sous-espaces vectoriels propres sont les droites vectorielles. Ce sont aussi des hyperplans vectoriels.
Dans une base
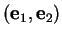 , une droite vectorielle
, une droite vectorielle 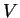 est donc caractérisée par une équation
est donc caractérisée par une équation
Comme
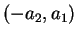 en est une solution non nulle,
en est une solution non nulle,
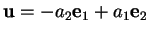 est une base de
est une base de 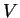 qui admet ainsi les équations paramétriques
qui admet ainsi les équations paramétriques
Une équation cartésienne
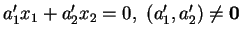 représente la même droite si et seulement si, avec les conventions admises plus haut,
représente la même droite si et seulement si, avec les conventions admises plus haut,
On retrouve cela en remarquant qu'elle doit être satisfaite par les composantes de 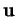 .
.
Remarque 1.5.11
Traditionnellement, en dimension
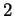
, les composantes sont notées
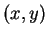
plutôt que
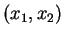
, ce qui allège d'ailleurs les écritures.
2002-12-17
![]() est de dimension
est de dimension ![]() , les seuls sous-espaces vectoriels propres sont les droites vectorielles. Ce sont aussi des hyperplans vectoriels.
, les seuls sous-espaces vectoriels propres sont les droites vectorielles. Ce sont aussi des hyperplans vectoriels.
![]() , une droite vectorielle
, une droite vectorielle ![]() est donc caractérisée par une équation
est donc caractérisée par une équation
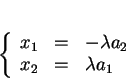
![]() représente la même droite si et seulement si, avec les conventions admises plus haut,
représente la même droite si et seulement si, avec les conventions admises plus haut,