suivant: 2.7.3 En dimension 2
monter: 2.7 Equations paramétriques et
précédent: 2.7.1 Equations paramétriques
Table des matières
Soient encore une variété affine
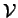 , de dimension
, de dimension 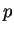 , et
, et
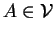 .
Considérons des équations cartésiennes
.
Considérons des équations cartésiennes
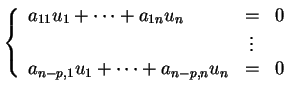 |
(2.5) |
décrivant
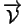 dans la base
dans la base
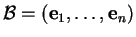 . Pour rappel, les vecteurs des coefficients de ces équations sont linéairement indépendants.
Comme plus haut, on désigne encore par
. Pour rappel, les vecteurs des coefficients de ces équations sont linéairement indépendants.
Comme plus haut, on désigne encore par 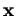 et
et 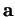 les coordonnées de
les coordonnées de  et
et  . Cette fois,
. Cette fois,  appartient à
appartient à
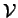 si et seulement si les composantes
si et seulement si les composantes
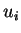 de
de
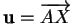 sont solutions de (13), c'est-à-dire si
En posant
on obtient ainsi des équations cartésiennes de
sont solutions de (13), c'est-à-dire si
En posant
on obtient ainsi des équations cartésiennes de
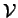 :
Inversement, on peut vérifier que les points dont les coordonnées sont solutions d'un système de
:
Inversement, on peut vérifier que les points dont les coordonnées sont solutions d'un système de 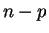 équations du premier degré indépendantes forment une variété
affine de dimension
équations du premier degré indépendantes forment une variété
affine de dimension 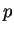 . Il est utile de noter que les équations homogènes associées sont alors des équations cartésiennes du sous-vectoriel directeur de cette
variété affine.
. Il est utile de noter que les équations homogènes associées sont alors des équations cartésiennes du sous-vectoriel directeur de cette
variété affine.




suivant: 2.7.3 En dimension 2
monter: 2.7 Equations paramétriques et
précédent: 2.7.1 Equations paramétriques
Table des matières
2002-12-17
![]() , de dimension
, de dimension ![]() , et
, et
![]() .
Considérons des équations cartésiennes
.
Considérons des équations cartésiennes