



suivant: 2.7.2 Equations cartésiennes
monter: 2.7 Equations paramétriques et
précédent: 2.7 Equations paramétriques et
Table des matières
Soient une variété affine (non vide)
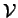 et
et
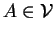 .
Si
.
Si
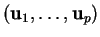 est une base de
est une base de
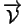 , alors
, alors  appartient à
appartient à
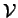 si et seulement si
si et seulement si
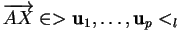 .
Ceci signifie que les point de
.
Ceci signifie que les point de
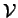 sont les
sont les  pour lesquels il existe
pour lesquels il existe
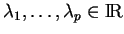 tels que
tels que
où
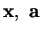 sont les coordonnées de
sont les coordonnées de  et
et  et où
et où
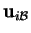 est le vecteur des composantes de
est le vecteur des composantes de 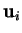 selon la base
selon la base
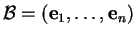 . Explicitée composante à composante, cette relation fournit des équations paramétriques de
. Explicitée composante à composante, cette relation fournit des équations paramétriques de
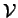 .
.
2002-12-17
![]() et
et
![]() .
Si
.
Si
![]() est une base de
est une base de
![]() , alors
, alors ![]() appartient à
appartient à
![]() si et seulement si
si et seulement si
![]() .
Ceci signifie que les point de
.
Ceci signifie que les point de
![]() sont les
sont les ![]() pour lesquels il existe
pour lesquels il existe
![]() tels que
tels que