suivant: 2.4 Variétés affines
monter: 2.3 Combinaisons affines
précédent: 2.3.4 Rapport de section
Table des matières
Le barycentre d'un ensemble de points pondérés peut se calculer par étapes, en les remplaçant par les barycentres de certains de leurs sous-sensembles.
Proposition 2.3.4
Soient une partition
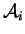
,
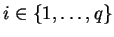
, d'un ensemble
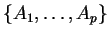
de points affectés de poids respectifs
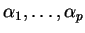
. On a
où
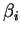
est la somme des poids des éléments de
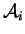
et
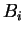
le barycentre de ces éléments,
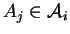
étant affecté du poids
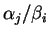
.
Preuve. Pour alléger l'écriture, nous détaillerons le cas d'une partition en deux sous-ensembles
Une origine quelconque 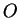 étant choisie, il vient, avec
D'où la conclusion.
étant choisie, il vient, avec
D'où la conclusion.
Remarque 2.3.5
Dans la Proposition
3.4, on suppose que les
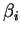
ne sont pas nuls. Il est facile d'adapter l'énoncé pour tenir compte
des
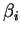
nuls. Ceci est laissé comme exercice au lecteur.
La Proposition 3.4 est, par exemple, utile en mécanique pour le calcul du centre de masse. En voici une application géométrique
très classique qui est l'occasion d'introduire un peu de vocabulaire. Trois points non alignés  ,
, 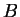 ,
, 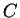 sont les sommets du triangle
sont les sommets du triangle
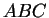 . Les segments
. Les segments
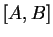 ,
,
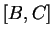 et
et
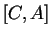 en sont les côtés.
La médiane relative à un sommet est la droite joignant ce sommet au milieu du côté opposé.
On a
en sont les côtés.
La médiane relative à un sommet est la droite joignant ce sommet au milieu du côté opposé.
On a
Il en résulte immédiatement que les médianes d'un triangle se coupent en son centre de gravité,
au deux tiers de chacune à partir de son sommet.




suivant: 2.4 Variétés affines
monter: 2.3 Combinaisons affines
précédent: 2.3.4 Rapport de section
Table des matières
2002-12-17
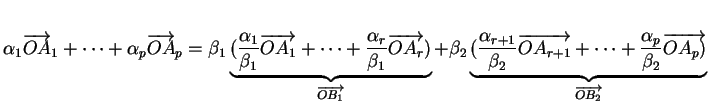
![]() ,
, ![]() ,
, ![]() sont les sommets du triangle
sont les sommets du triangle
![]() . Les segments
. Les segments
![]() ,
,
![]() et
et
![]() en sont les côtés.
La médiane relative à un sommet est la droite joignant ce sommet au milieu du côté opposé.
On a
en sont les côtés.
La médiane relative à un sommet est la droite joignant ce sommet au milieu du côté opposé.
On a