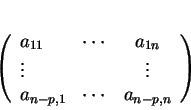suivant: 1.5.4.1 Les hyperplans vectoriels
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.3 Equations paramétriques
Table des matières
Soit une une base
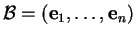 de
de  . On cherche des équations homogènes du premier degré
. On cherche des équations homogènes du premier degré
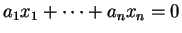 |
(1.3) |
en les composantes
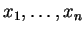 de
de
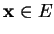 selon
selon
 qui caractérisent le fait que
qui caractérisent le fait que 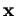 appartienne à un sous-espace vectoriel
appartienne à un sous-espace vectoriel
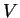 de
de  donné.
donné.
L'équation (3) est complètement déterminée par le vecteur
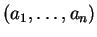 de ses coefficients. Quand on additionne membre à membre des
équations telles que (3), ou quand on en multiplie les membres par un même nombre, les vecteurs des coefficients subissent les mêmes opérations.
de ses coefficients. Quand on additionne membre à membre des
équations telles que (3), ou quand on en multiplie les membres par un même nombre, les vecteurs des coefficients subissent les mêmes opérations.
On désigne par
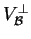 la partie de
la partie de
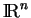 formée par les vecteurs des coefficients des équations de la forme (3)
qui sont satisfaites par les composantes des éléments de
formée par les vecteurs des coefficients des équations de la forme (3)
qui sont satisfaites par les composantes des éléments de 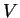 (dans la base
(dans la base
 ).
C'est un sous-espace vectoriel de
).
C'est un sous-espace vectoriel de
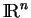 car en additionnant ou en multipliant par des nombres des équations satisfaites par les composantes
des éléments de
car en additionnant ou en multipliant par des nombres des équations satisfaites par les composantes
des éléments de 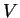 , on en obtient qui le sont aussi.
, on en obtient qui le sont aussi.
Preuve. Il existe une base
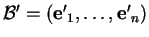 de
de  dont les premiers éléments
dont les premiers éléments
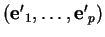 forment une base de
forment une base de 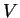 (Proposition 5.8). En particulier,
(Proposition 5.8). En particulier,
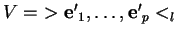 et
et
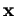 de composantes
de composantes
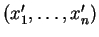 dans la base
dans la base
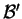 appartient à
appartient à 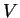 si et seulement si
si et seulement si
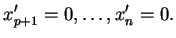 |
(1.4) |
Lors du passage de la base
 à la base
à la base
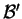 , les
composantes de
, les
composantes de 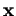 selon
selon
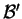 s'expriment au moyen de fonctions
homogènes du premier degré en ses composantes dans
s'expriment au moyen de fonctions
homogènes du premier degré en ses composantes dans
 ,
dont les vecteurs des coefficients sont linéairement indépendants (Proposition 4.6).
Les conditions (4), c'est-à-dire le fait que
,
dont les vecteurs des coefficients sont linéairement indépendants (Proposition 4.6).
Les conditions (4), c'est-à-dire le fait que
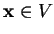 , équivalent donc aux
, équivalent donc aux 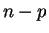 équations indépendantes
équations indépendantes
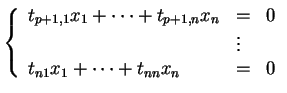 |
(1.5) |
Ceci montre que la dimension de
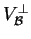 est au moins égale à
est au moins égale à 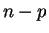 .
.
Supposons par ailleurs que
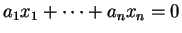 |
(1.6) |
quand
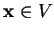 . Puisque les
. Puisque les 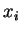 sont, semblablement, des fonctions homogènes du premier degré
en les
sont, semblablement, des fonctions homogènes du premier degré
en les 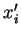 , cette condition prend la forme
Elle doit être satisfaite pour
, cette condition prend la forme
Elle doit être satisfaite pour
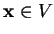 , c'est-à-dire lorsque (4) est vérifié.
Cela revient à demander que
donc que
, c'est-à-dire lorsque (4) est vérifié.
Cela revient à demander que
donc que
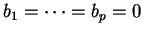 . L'équation (6) s'écrit donc encore
soit
Le vecteur de ses coefficients est donc combinaison linéaire de ceux des équations (5).
Par conséquent, la dimension de
. L'équation (6) s'écrit donc encore
soit
Le vecteur de ses coefficients est donc combinaison linéaire de ceux des équations (5).
Par conséquent, la dimension de
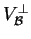 est
est 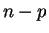 .
.
La proposition ci-dessus montre que les sous-espaces vectoriels 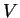 de dimension
de dimension 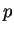 de
de  sont
exactement décrits par les systèmes de
sont
exactement décrits par les systèmes de 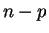 équations homogènes du premier degré indépendantes:
équations homogènes du premier degré indépendantes:
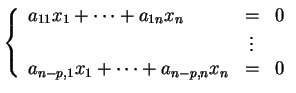 |
(1.7) |
les vecteurs formés par les lignes du tableau
étant linéairement indépendants. De telles équations sont appelées cartésiennes. De plus, toute équation linéaire satisfaite par les composantes des
éléments de
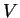 est nécessairement combinaison linéaire des équations (7).
est nécessairement combinaison linéaire des équations (7).
Sous-sections




suivant: 1.5.4.1 Les hyperplans vectoriels
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.3 Equations paramétriques
Table des matières
2002-12-17
![]() de
de ![]() . On cherche des équations homogènes du premier degré
. On cherche des équations homogènes du premier degré
![]() de ses coefficients. Quand on additionne membre à membre des
équations telles que (3), ou quand on en multiplie les membres par un même nombre, les vecteurs des coefficients subissent les mêmes opérations.
de ses coefficients. Quand on additionne membre à membre des
équations telles que (3), ou quand on en multiplie les membres par un même nombre, les vecteurs des coefficients subissent les mêmes opérations.
![]() la partie de
la partie de
![]() formée par les vecteurs des coefficients des équations de la forme (3)
qui sont satisfaites par les composantes des éléments de
formée par les vecteurs des coefficients des équations de la forme (3)
qui sont satisfaites par les composantes des éléments de ![]() (dans la base
(dans la base
![]() ).
C'est un sous-espace vectoriel de
).
C'est un sous-espace vectoriel de
![]() car en additionnant ou en multipliant par des nombres des équations satisfaites par les composantes
des éléments de
car en additionnant ou en multipliant par des nombres des équations satisfaites par les composantes
des éléments de ![]() , on en obtient qui le sont aussi.
, on en obtient qui le sont aussi.
![]() de dimension
de dimension ![]() de
de ![]() sont
exactement décrits par les systèmes de
sont
exactement décrits par les systèmes de ![]() équations homogènes du premier degré indépendantes:
équations homogènes du premier degré indépendantes: