



suivant: 1.5.3 Equations paramétriques
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.1 Définition
Table des matières
Exemple 1.5.2
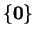
et

sont des sous-espaces vectoriels de

.
C'est immédiat. Il est commode, et sans réel danger de confusion, de noter 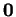 le sous-espace
le sous-espace
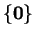 .
Un sous-espace vectoriel de
.
Un sous-espace vectoriel de  qui n'est ni
qui n'est ni
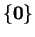 , ni
, ni  est dit propre.
est dit propre.
Exemple 1.5.3
L'enveloppe linéaire d'éléments de

.
Les formules
montrent que l'ensemble des combinaisons linéaires de
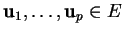 est un sous-espace vectoriel de
est un sous-espace vectoriel de  .
On le note
On l'appelle l'enveloppe linéaire de
.
On le note
On l'appelle l'enveloppe linéaire de
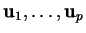 ; on dit aussi qu'il est engendré par
; on dit aussi qu'il est engendré par
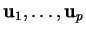 .
.
Exemple 1.5.4
L'ensemble des solutions d'équations homogènes du premier degré.
Vu la Proposition 4.5, les éléments de  dont les composantes
dont les composantes
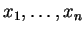 dans une base donnée vérifient un système d'équations linéaires
homogènes
forment un sous-espace vectoriel de
dans une base donnée vérifient un système d'équations linéaires
homogènes
forment un sous-espace vectoriel de  .
.
Les deux exemples ci-dessus donnent des moyens généraux de construire des sous-espaces vectoriels. Nous allons voir qu'en fait,
tout sous-espace vectoriel peut être décrit par l'un et l'autre. Dans le premier cas, nous obtiendrons des équations paramétriques,
dans le second, des équations cartésiennes pour les sous-espaces vectoriels. Voici d'abord deux exemples supplémentaires de sous-espaces vectoriels.
Exemple 1.5.5
Les polynômes.
Les polynômes
en la variable 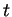 forment un sous-espace vectoriel de l'espace
forment un sous-espace vectoriel de l'espace
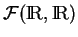 des fonctions de
des fonctions de
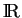 dans lui-même (voir l'Exemple 3.4)
car la somme et le produit par un nombre de polynômes sont encore des polynômes.
De même, les polynômes de degré inférieur ou égal à un nombre donné
dans lui-même (voir l'Exemple 3.4)
car la somme et le produit par un nombre de polynômes sont encore des polynômes.
De même, les polynômes de degré inférieur ou égal à un nombre donné 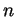 constituent aussi un sous-espace vectoriel
constituent aussi un sous-espace vectoriel
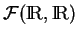 .
.
L'espace des polynômes est utilisé en CAGD (Computer Aided Geometric Design), notamment dans l'étude des courbes de Béziers.
A la base naturelle formée des 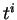 , on préfère alors certaines bases plus adaptées aux problèmes rencontrés,
comme par exemple celle constituée des polynômes de Bernstein.
, on préfère alors certaines bases plus adaptées aux problèmes rencontrés,
comme par exemple celle constituée des polynômes de Bernstein.
Exemple 1.5.6
Les applications linéaires.
Soient des espaces vectoriels 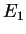 et
et 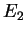 . Une application
. Une application
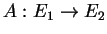 est linéaire si elle respecte la somme et la multiplication scalaire, ce
qu'on peut résumer par
Par exemple, le passage aux coordonnées est une bijection linéaire (Proposition 4.5).
est linéaire si elle respecte la somme et la multiplication scalaire, ce
qu'on peut résumer par
Par exemple, le passage aux coordonnées est une bijection linéaire (Proposition 4.5).
Muni des opérations introduites dans l'Exemple 3.4, l'espace
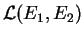 des applications linéaires de
des applications linéaires de 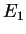 dans
dans 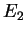 est un sous-espace vectoriel de
est un sous-espace vectoriel de
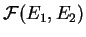 . Les vérifications sont faciles. Par exemple, si
. Les vérifications sont faciles. Par exemple, si 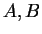 sont linéaires, alors
sont linéaires, alors
L'espace
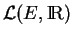 se note
se note 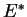 . On l'appelle le dual
de
. On l'appelle le dual
de  .
.




suivant: 1.5.3 Equations paramétriques
monter: 1.5 Sous-espaces vectoriels
précédent: 1.5.1 Définition
Table des matières
2002-12-17
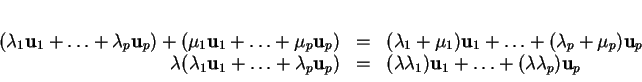
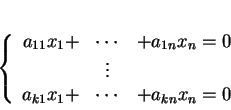
![]() , on préfère alors certaines bases plus adaptées aux problèmes rencontrés,
comme par exemple celle constituée des polynômes de Bernstein.
, on préfère alors certaines bases plus adaptées aux problèmes rencontrés,
comme par exemple celle constituée des polynômes de Bernstein.
![]() des applications linéaires de
des applications linéaires de ![]() dans
dans ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de
![]() . Les vérifications sont faciles. Par exemple, si
. Les vérifications sont faciles. Par exemple, si ![]() sont linéaires, alors
sont linéaires, alors
![]() se note
se note ![]() . On l'appelle le dual
de
. On l'appelle le dual
de ![]() .
.