suivant: 1.4 Combinaisons linéaires, bases
monter: 1 Introduction aux espaces
précédent: 1.2 Les axiomes
Table des matières
Exemple 1.3.1
L'ensemble
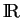
L'addition et la multiplication des nombres réels font évidemment de
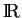 un espace vectoriel.
un espace vectoriel.
On note
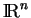 l'ensemble de tous les n-uples
l'ensemble de tous les n-uples
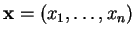 de nombres réels
de nombres réels
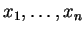 .
Les nombres
.
Les nombres 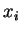 sont les composantes de
sont les composantes de 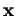 . Il faut bien prendre conscience de ce que
. Il faut bien prendre conscience de ce que
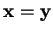 si et seulement si
si et seulement si
L'addition et la multiplication scalaire de
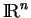 sont définies composantes à composantes, c'est-à-dire par
Il est clair que
sont définies composantes à composantes, c'est-à-dire par
Il est clair que
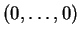 est un élément neutre pour cette addition et que l'opposé est donné par
est un élément neutre pour cette addition et que l'opposé est donné par
Les opérations introduites sur
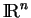 se ramenant aux opérations de mêmes noms sur les composantes, il est immédiat qu'elles font de
se ramenant aux opérations de mêmes noms sur les composantes, il est immédiat qu'elles font de
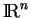 un espace vectoriel.
un espace vectoriel.
Exemple 1.3.3
Le produit cartésien d'espaces vectoriels
L'exemple précédent se généralise de la manière suivante. Soient des espaces vectoriels
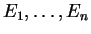 . On note
. On note
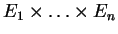 l'ensemble des
suites
l'ensemble des
suites
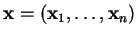 , où
, où
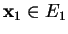 ,...,
,...,
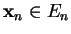 . C'est un espace vectoriel pour les opérations définies par
. C'est un espace vectoriel pour les opérations définies par
Une fonction 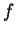 d'un ensemble
d'un ensemble  dans un ensemble
dans un ensemble  est une loi qui associe un élément
est une loi qui associe un élément 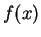 de
de  à chaque élément
à chaque élément 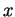 de
de  .
L'ensemble de ces fonctions est désigné par
.
L'ensemble de ces fonctions est désigné par
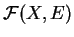 . Si
. Si  est un espace vectoriel, alors
est un espace vectoriel, alors
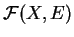 en est un aussi, quand on le munit des
opérations définies par
en est un aussi, quand on le munit des
opérations définies par
Les vérifications sont faciles. Examinons par exemple l'associativité de la multiplication scalaire. Il faut vérifier que si
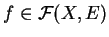 et si
et si
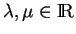 , alors les fonctions
, alors les fonctions
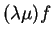 et
et
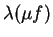 sont égales. Or, pour tout
sont égales. Or, pour tout 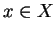 , on a
, on a
en utilisant l'associativité de la multiplication scalaire de  pour la seconde égalité. L'élément neutre est la fonction
pour la seconde égalité. L'élément neutre est la fonction
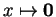 et l'opposé de
et l'opposé de
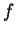 est la fonction
est la fonction
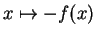 .
.




suivant: 1.4 Combinaisons linéaires, bases
monter: 1 Introduction aux espaces
précédent: 1.2 Les axiomes
Table des matières
2002-12-17
![]() l'ensemble de tous les n-uples
l'ensemble de tous les n-uples
![]() de nombres réels
de nombres réels
![]() .
Les nombres
.
Les nombres ![]() sont les composantes de
sont les composantes de ![]() . Il faut bien prendre conscience de ce que
. Il faut bien prendre conscience de ce que
![]() si et seulement si
si et seulement si