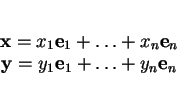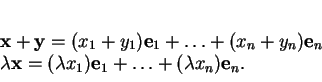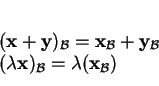1.4.3 Composantes

Soit une base ${\mathcal B}=({\bf e}_1, \ldots , {\bf e}_n)$ de $E$. Par définition de la notion de base, tout élément ${\bf x}\in E$ s'écrit de façon unique comme combinaison linéaire des éléments de ${\mathcal B}$: il existe un seul jeu ${\bf x}_{\mathcal B} = (x_1, \ldots ,x_n)$ de nombres réels tels que

$${\bf x} = x_1{\bf e}_1+\ldots+x_n{\bf e}_n.$$

On les appelle les composantes de x dans, ou selon, la base ${\mathcal B}$. Observons que les composantes de ${\bf0}$ sont toutes nulles.

Remarque 1.4.4   Vu (1), la signification du mot composantes introduit dans l'exemple 3.2 est la même que celle donnée ici.

Proposition 1.4.5   Le passage aux composantes

$${\bf x}\in E \mapsto {\bf x}_{\mathcal B}\in {\rm I\!R}¬^n$$

est une correspondance biunivoque. Il est linéaire: il respecte l'addition et la multiplication scalaire. En particulier, il transforme des vecteurs linéairement indépendants (resp. dépendants) en des vecteurs linéairement indépendants (resp. dépendants).

Preuve. Il est clair que la correspondance ${\bf x}\in E \mapsto {\bf x}_{\mathcal B}\in {\rm I\!R}¬^n$ est biunivoque: deux vecteurs de mêmes composantes sont égaux et tout élément de ${\rm I\!R}^n$ est formé des composantes d'un élément de $E$. Elle est linéaire. En effet, de

$$% latex2html id marker 27841\begin{array}{c} {\bf x} = x_1... ...n \\ {\bf y} = y_1{\bf e}_1+\ldots+y_n{\bf e}_n \end{array}$$

on tire , en additionnant membre à membre ou en multipliant par le nombre $\lambda$,

$$% latex2html id marker 27845\begin{array}{l} {\bf x}+{\bf ... ...mbda x_1){\bf e}_1+\ldots+(\lambda x_n){\bf e}_n. \end{array}$$

Par conséquent

$$% latex2html id marker 27847\begin{array}{l} ({\bf x}+{\bf... ...x})_{\mathcal B} = \lambda ({\bf x}_{\mathcal B}) \end{array}$$

comme annoncé. Comme elle est biunivoque et que les composantes de $\bf0$ sont nulles, elle conserve donc l'indépendance et la dépendance linéaires. $\qed$