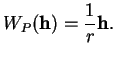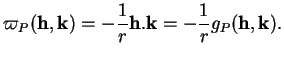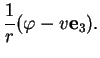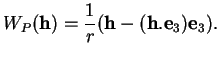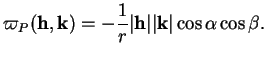suivant: 7.5.2.2 Expression de
monter: 7.5.2 La seconde forme
précédent: 7.5.2 La seconde forme
Table des matières
La dérivée de 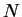 dans la direction de
dans la direction de
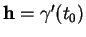 est, par définition, la dérivée en
est, par définition, la dérivée en 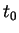 de
de
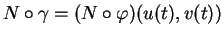 . Elle vaut donc
. Elle vaut donc
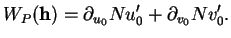 |
(7.7) |
(
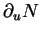 et
et
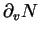 désignent les dérivées de
désignent les dérivées de
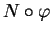 par rapport à
par rapport à 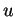 et
et 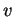 respectivement.)
En particulier, cette expression montre que
respectivement.)
En particulier, cette expression montre que
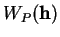 ne dépend que
de
ne dépend que
de 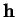 et non de l'arc de courbe
et non de l'arc de courbe 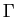 choisi pour l'évaluer.
Elle montre également que
choisi pour l'évaluer.
Elle montre également que
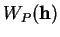 dépend linéairement de
dépend linéairement de
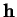 .
.
Exemple 7.5.6
Sphère rapportée aux coordonnées sphériques
Poursuivons l'exemple (5.1) en notant 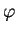 le paramétrage
par les coordonnées sphériques. La normale (37) vaut
le paramétrage
par les coordonnées sphériques. La normale (37) vaut
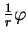 . Par conséquent, l'application de Weingarten de
la sphère est donnée par
C'est donc un multiple de l'identité. La seconde forme fondamentale
est alors donnée par
. Par conséquent, l'application de Weingarten de
la sphère est donnée par
C'est donc un multiple de l'identité. La seconde forme fondamentale
est alors donnée par
Exemple 7.5.7
Cylindre circulaire droit
Calculons de même l'application de Weingarten du cylindre circulaire
droit dans le paramétrage 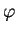 donné par (38). En le
point
donné par (38). En le
point  de paramètres
de paramètres 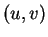 , la normale (37) vaut
Par conséquent,
Si
, la normale (37) vaut
Par conséquent,
Si  et
et 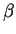 désignent les angles non orientés que
font respectivement les tangentes en
désignent les angles non orientés que
font respectivement les tangentes en  de vecteur-directeurs
de vecteur-directeurs 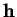 et
et 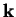 avec la tangente orthogonale aux génératrices , on a donc
avec la tangente orthogonale aux génératrices , on a donc




suivant: 7.5.2.2 Expression de
monter: 7.5.2 La seconde forme
précédent: 7.5.2 La seconde forme
Table des matières
2002-12-17