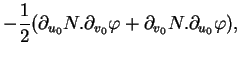suivant: 7.5.3 Le théorème de
monter: 7.5.2 La seconde forme
précédent: 7.5.2.1 Expression de
Table des matières
On peut également calculer 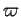 au moyen d'un paramétrage de
au moyen d'un paramétrage de
 . Cela va d'ailleurs permettre de vérifier qu'il est symétrique en
ses arguments.
. Cela va d'ailleurs permettre de vérifier qu'il est symétrique en
ses arguments.
Proposition 7.5.8
Si les composantes de
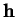
et
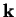
dans la base
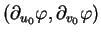
sont
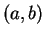
et
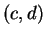
respectivement, alors
où
En particulier,
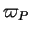
est symétrique.
Preuve. On a
Donc, vu (38)
Mais, comme
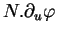 et
et
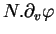 sont
nuls, on a toujours
sont
nuls, on a toujours
D'où la formule annoncée.
On rencontre souvent l'écriture
qui est l'analogue pour 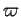 de la formule du célèbre ``
de la formule du célèbre ``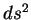 ".
".




suivant: 7.5.3 Le théorème de
monter: 7.5.2 La seconde forme
précédent: 7.5.2.1 Expression de
Table des matières
2002-12-17