



suivant: 7.4 Plan tangent, orientation
monter: 7.3 Equation cartésienne -
précédent: 7.3 Equation cartésienne -
Table des matières
Si  est l'image d'un paramétrage par des coordonnées
alors
est une équation cartésienne de
est l'image d'un paramétrage par des coordonnées
alors
est une équation cartésienne de  dans l'ouvert
dans l'ouvert 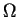 formé des
points de coordonnées dans
formé des
points de coordonnées dans
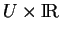 .
.
La sphère 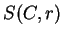 de centre
de centre 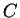 et de rayon
et de rayon 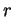 est une surface. En
effet, dans un repère orthonormé de
est une surface. En
effet, dans un repère orthonormé de
 , ses points sont
caractérisés par la condition
, ses points sont
caractérisés par la condition
où 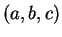 sont les coordonnées de
sont les coordonnées de 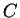 . La fonction
est une équation cartésienne de
. La fonction
est une équation cartésienne de 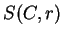 dans le complémentaire de
dans le complémentaire de
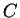 car son gradient en
car son gradient en  est le vecteur
est le vecteur
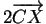 .
.
2002-12-17
![]() de centre
de centre ![]() et de rayon
et de rayon ![]() est une surface. En
effet, dans un repère orthonormé de
est une surface. En
effet, dans un repère orthonormé de
![]() , ses points sont
caractérisés par la condition
, ses points sont
caractérisés par la condition