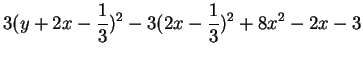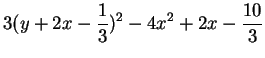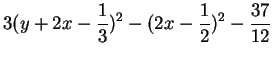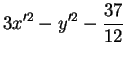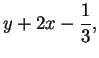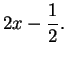suivant: 7 Surfaces
monter: 6.4.3.2 Classification des courbes
précédent: 6.4.3.2.2 Discussion
Table des matières
En combinant ces deux remarques et en changeant éventuellement de signe les deux membres de l'équation, on met en évidence
trois genres de courbes du second degré:
Les différents genres se subdivisent encore selon le signe de 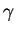 conduisant à la classification
à présent facile à obtenir:
conduisant à la classification
à présent facile à obtenir:
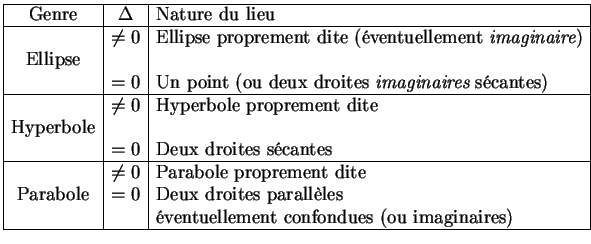 |
(6.9) |
Les noms entre parenthèse indiquent ce que serait le lieu si on acceptait des coordonnées complexes.
La distinction entre une ellipse proprement dite non vide et une ellipse proprement dite imaginaire
ne peut se faire sur la seule inspection du signe
de 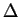 . En effet, celui-ci change lorsqu'on change le signe de tous les coefficients de l'équation.
On peut vérifier que l'ellipse n'est pas vide lorsque
. En effet, celui-ci change lorsqu'on change le signe de tous les coefficients de l'équation.
On peut vérifier que l'ellipse n'est pas vide lorsque
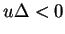 ou
ou
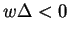 et qu'elle est imaginaire
si l'un de ces nombres est positif.
et qu'elle est imaginaire
si l'un de ces nombres est positif.
Corollaire 6.4.7
Si
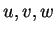
ne sont pas tous nuls, le polynôme
est le produit de deux polynômes du premier degré, éventuellement à coefficients complexes, si et seulement si
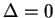
.
On dit que le lieu des points décrits en coordonnées par l'équation (30) quand 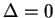 est une conique dégénérée. Quand il n'est pas vide et que
est une conique dégénérée. Quand il n'est pas vide et que
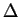 n'est pas nul, c'est une conique proprement dite; l'équation (30) en est alors une équation cartésienne comme on le vérifie facilement à
partir des équations canoniques.
n'est pas nul, c'est une conique proprement dite; l'équation (30) en est alors une équation cartésienne comme on le vérifie facilement à
partir des équations canoniques.
D'après le tableau (31) et le commentaire qui le suit, pour déterminer la nature du lieu des points dont les coordonnées sont les solutions
d'une équation du second degré, il suffit d'évaluer le signe des nombres
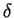 et
et 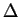 , sans nécessairement procéder à la réduction à la forme canonique. Par exemple, l'équation
, sans nécessairement procéder à la réduction à la forme canonique. Par exemple, l'équation
est celle d'une hyperbole (proprement dite) puisque
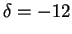 et
et
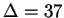 .
.
Pour réduire l'équation à la forme canonique, on cherche à diagonaliser la matrice 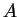 par une rotation des axes du repère, puis on translate si nécessaire
l'origine du repère pour éliminer les termes du premier degré superflus. Si l'on ne souhaite pas spécialement un repère orthonormé, on peut plus directement
compléter les carrés, comme illustré sur l'équation ci-dessus: on obtient par exemple
par une rotation des axes du repère, puis on translate si nécessaire
l'origine du repère pour éliminer les termes du premier degré superflus. Si l'on ne souhaite pas spécialement un repère orthonormé, on peut plus directement
compléter les carrés, comme illustré sur l'équation ci-dessus: on obtient par exemple
en posant
Cette manière de procéder consiste à collecter les termes en une des variables figurant au carré dans l'équation (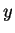 dans l'exemple ci-dessus) et à les regarder
comme les deux premiers termes d'un carré parfait. On complète celui-ci (comme dans la remarque a) plus haut), ce qui laisse des termes contenant uniquement la
seconde variable. Si celle-ci figure au second degré, on lui applique le même traitement. Sinon, elle figure au plus au premier degré et la réduction est terminée.
Si ni
dans l'exemple ci-dessus) et à les regarder
comme les deux premiers termes d'un carré parfait. On complète celui-ci (comme dans la remarque a) plus haut), ce qui laisse des termes contenant uniquement la
seconde variable. Si celle-ci figure au second degré, on lui applique le même traitement. Sinon, elle figure au plus au premier degré et la réduction est terminée.
Si ni
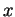 ni
ni 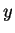 ne figurent au carré, il y a nécessairement un terme en
ne figurent au carré, il y a nécessairement un terme en 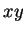 . Comme
en posant
. Comme
en posant 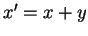 et
et 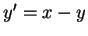 , on fait apparaître des carrés avec lesquels on peut appliquer ensuite la méthode.
, on fait apparaître des carrés avec lesquels on peut appliquer ensuite la méthode.




suivant: 7 Surfaces
monter: 6.4.3.2 Classification des courbes
précédent: 6.4.3.2.2 Discussion
Table des matières
2002-12-17
![]() est une conique dégénérée. Quand il n'est pas vide et que
est une conique dégénérée. Quand il n'est pas vide et que
![]() n'est pas nul, c'est une conique proprement dite; l'équation (30) en est alors une équation cartésienne comme on le vérifie facilement à
partir des équations canoniques.
n'est pas nul, c'est une conique proprement dite; l'équation (30) en est alors une équation cartésienne comme on le vérifie facilement à
partir des équations canoniques.
![]() et
et ![]() , sans nécessairement procéder à la réduction à la forme canonique. Par exemple, l'équation
, sans nécessairement procéder à la réduction à la forme canonique. Par exemple, l'équation
![]() par une rotation des axes du repère, puis on translate si nécessaire
l'origine du repère pour éliminer les termes du premier degré superflus. Si l'on ne souhaite pas spécialement un repère orthonormé, on peut plus directement
compléter les carrés, comme illustré sur l'équation ci-dessus: on obtient par exemple
par une rotation des axes du repère, puis on translate si nécessaire
l'origine du repère pour éliminer les termes du premier degré superflus. Si l'on ne souhaite pas spécialement un repère orthonormé, on peut plus directement
compléter les carrés, comme illustré sur l'équation ci-dessus: on obtient par exemple
![$\displaystyle 3[y^2+2(2x-\frac{1}{3})y]+8x^2-2x-3$](img2042.gif)