1.4.2 Bases

Il est utile de savoir si, plus généralement, on peut décrire tout élément de $E$ comme combinaison linéaire d'éléments ${\bf u}_1$,..., ${\bf u}_p$ bien choisis. D'autre part, il est également utile de savoir dans quelle mesure l'écriture éventuelle d'un élément de $E$ comme combinaison linéaire des ${\bf u}_i$ est unique.

Proposition 1.4.1   Soient des éléments ${\bf u}_1$,..., ${\bf u}_p$ de $E$. Les propriétés suivantes sont équivalentes.

(i)Un élément de $E$ s'exprime de deux façons différentes comme combinaison linéaire de ${\bf u}_1$,..., ${\bf u}_p$.

(ii)Il existe des nombres non tous nuls $\alpha_1$,..., $\alpha_p$ tels que

$$\alpha_1{\bf u}_1+ \ldots +\alpha_p{\bf u}_p={\bf0}.$$

(iii)Un des ${\bf u}_i$ est combinaison linéaire des autres.

Preuve. (i) implique (ii). En effet, si

$$\lambda_1{\bf u}_1+ \ldots +\lambda_p{\bf u}_p=\mu_1{\bf u}_1+ \ldots +\mu_p{\bf u}_p$$

avec $\lambda_i \ne \mu_i$ pour au moins un $i$, alors, en soustrayant, il vient

$$(\lambda_1-\mu_1){\bf u}_1+ \ldots +(\lambda_p-\mu_p){\bf u}_p={\bf0}$$

où l'un des coefficients $\lambda_i-\mu_i$ n'est pas nul.

(ii) implique (iii). En effet, si, par exemple $\alpha_1$ n'est pas nul, alors

$${\bf u}_1=(-\frac {\alpha_2}{\alpha_1}){\bf u}_2+ \ldots +(-\frac {\alpha_p}{\alpha_1}){\bf u}_p.$$

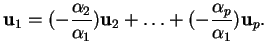
(iii) implique (i). C'est évident! $\qed$

On dit de vecteurs ${\bf u}_1$,..., ${\bf u}_p$ qui vérifient l'une des propriétés équivalentes ci-dessus qu'ils sont linéairement dépendants.

S'ils ne les vérifient pas, ils sont linéairement indépendants. Dans ce cas, l'écriture éventuelle d'un élément de $E$ comme combinaison linéaire des ${\bf u}_i$ est unique. Si, en plus, tout élément de $E$ est combinaison linéaire des ${\bf u}_i$, alors, par définition, ${\bf u}_1$,..., ${\bf u}_p$ forment une base de $E$. Par exemple, $({\overrightarrow{e}_1}, \ldots ,{\overrightarrow{e}_n})$ est une base de ${\rm I\!R}^n$, qu'on appelle la base canonique.

Théorème 1.4.2   Soient des éléments ${\bf u}_1$,..., ${\bf u}_p$ de $E$ et des combinaisons linéaires ${\bf v}_1$,..., ${\bf v}_q$ des ${\bf u}_i$. Si $q > p$, alors ${\bf v}_1$,..., ${\bf v}_q$ sont linéairement dépendants.

Preuve. On procède par récurrence sur $p$.

Pour $p=1$, on a ${\bf v}_1=\lambda_1 {\bf u}_1$,..., ${\bf v}_q=\lambda_q {\bf u}_1$, avec $q \ge 2$. En particulier, $\lambda_2 {\bf v}_1-\lambda_1 {\bf v}_2={\bf0}$. Si $\lambda_1 \ne 0$, les ${\bf v}_i$ sont donc linéairement dépendants. Si $\lambda_1 = 0$, ils le sont aussi car alors ${\bf v}_1={\bf0}$.

Passons de $p$ à $p+1$. Ecrivons les combinaisons linéaires ${\bf v}_i$ en mettant en évidence le coefficient de ${\bf u}_1$:

$${\bf v}_i=\lambda_i{\bf u}_1+{\bf w}_i, \ i=1, \ldots,q,$$

où les ${\bf w}_i$ sont combinaisons linéaires de ${\bf u}_2$,..., ${\bf u}_{p+1}$. Si les $\lambda_i$ sont tous nuls, alors ${\bf v}_1$,..., ${\bf v}_q$ sont combinaisons linéaires de $p$ vecteurs. Par hypothèse de récurrence, ils sont donc linéairement dépendants. Si l'un des $\lambda_i$ n'est pas nul, par exemple $\lambda_1$, alors, par hypothèse de récurrence, les vecteurs

$$\lambda_1{\bf v}_i-\lambda_i{\bf v}_1=\lambda_1{\bf w}_i-\lambda_i{\bf w}_1, \ i=2, \ldots ,q,$$

sont linéairement dépendants car ils sont combinaisons linéaires de ${\bf u}_2$,..., ${\bf u}_{p+1}$ et sont en nombre $q-1 >p$: il existe des nombres non tous nuls $\alpha_2$,...,$\alpha_q$ tels que

$$\alpha_2(\lambda_1{\bf v}_2-\lambda_2{\bf v}_1)+ \ldots + \alpha_q(\lambda_1{\bf v}_q-\lambda_q{\bf v}_1) = {\bf0}.$$

Ceci s'écrit

$$-(\alpha_2\lambda_2 + \ldots + \alph... ..._1 + \alpha_2\lambda_1{\bf v}_2+ \ldots + \alpha_q\lambda_1{\bf v}_q = {\bf0}.$$

Les ${\bf v}_i$ sont donc linéairement dépendants puisqu'un des nombres $\alpha_2\lambda_1$,..., $\alpha_q\lambda_1$ n'est pas nul. $\qed$

Corollaire 1.4.3   Les bases de $E$ ont toutes le même nombre d'éléments.

On dit que $E$ est de dimension finie s'il admet une base ${\mathcal B}=({\bf e}_1, \ldots , {\bf e}_n)$, auquel cas le nombre $n$ d'éléments de ${\mathcal B}$, indépendant de ${\mathcal B}$, s'appelle la dimension de $E$ et on le note ${\rm dim}\ E$. Par exemple, ${\rm I\!R}^n$ est de dimension $n$.

Avertissement: Dans la suite, sauf mention explicite du contraire, les espaces vectoriels considérés sont supposés de dimension finie.