


suivant: 7 Inégalité isopérimétrique
monter: 6.2.4 Courbure de Gauss
précédent: 6.2.4 Courbure de Gauss
Table des matières
Soit
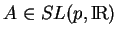 . Commençons par dériver la normale unitaire (17) dans la direction de
. Commençons par dériver la normale unitaire (17) dans la direction de
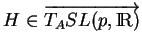 . On obtient ainsi facilement l'application de Weingarten de
. On obtient ainsi facilement l'application de Weingarten de
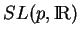 :
En particulier la seconde forme fondamentale de
:
En particulier la seconde forme fondamentale de
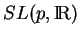 est
Afin de calculer le déterminant de
est
Afin de calculer le déterminant de 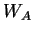 , nous allons procéder à quelques transformations.
Elles ont pour effet de remplacer
, nous allons procéder à quelques transformations.
Elles ont pour effet de remplacer 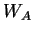 par des applications de même déterminant mais d'expression plus simple.
La première consiste à se ramener à l'espace tangent
par des applications de même déterminant mais d'expression plus simple.
La première consiste à se ramener à l'espace tangent
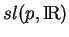 en
en 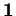 . En notant
. En notant 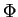 l'application
l'application
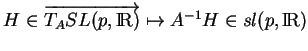 , on obtient
où
, on obtient
où
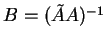 . La seconde transformation exploite le fait que l'on peut donner à
. La seconde transformation exploite le fait que l'on peut donner à 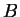 , qui est une matrice symétrique définie positive, une forme diagonale
, qui est une matrice symétrique définie positive, une forme diagonale 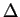 au moyen d'une matrice orthogonale
au moyen d'une matrice orthogonale 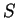 :
Les nombres
:
Les nombres 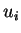 sont positifs et leur produit vaut
sont positifs et leur produit vaut 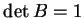 .
L'application linéaire
.
L'application linéaire
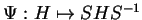 stabilise l'espace des matrices de trace nulle.
De plus,
stabilise l'espace des matrices de trace nulle.
De plus,
Proposition 54
La courbure de Gauss de
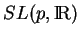
en
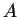
est
En particulier, elle atteint ses valeurs extrêmes sur
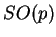
, où elle vaut
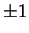
.
Pour calculer
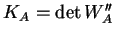 , nous allons décomposer
, nous allons décomposer
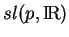 en somme directe
de sous-espaces stables pour
en somme directe
de sous-espaces stables pour 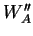 . Le déterminant de ce dernier est le produit des déterminants de ses restrictions aux termes de cettte somme:
De plus, afin d'alléger les écritures, nous allons d'abord calculer le déterminant de
. Le déterminant de ce dernier est le produit des déterminants de ses restrictions aux termes de cettte somme:
De plus, afin d'alléger les écritures, nous allons d'abord calculer le déterminant de
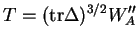 qu'il suffira ensuite de diviser par une puissance appropriée de
qu'il suffira ensuite de diviser par une puissance appropriée de
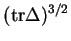 , la dimension
, la dimension 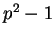 de
de
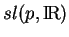 , pour obtenir
, pour obtenir 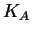 .
.
Pour 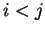 ,
, 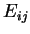 est formé des matrices
est formé des matrices 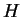 de trace nulle dont les éléments
de trace nulle dont les éléments
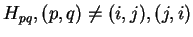 , sont nuls.
C'est un espace de dimension
, sont nuls.
C'est un espace de dimension 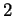 admettant une base
admettant une base 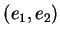 , où
, où
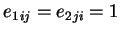 et
et
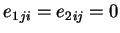 . Dans celle-ci, la restriction de
. Dans celle-ci, la restriction de 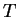 à
à 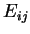 est représentée par la matrice
est représentée par la matrice
où
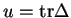 .
.
L'espace 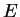 est formé des matrices diagonales
est formé des matrices diagonales
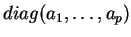 de trace nulle. Il admet la base
de trace nulle. Il admet la base
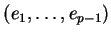 dans laquelle
dans laquelle 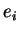 a un
a un 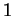 à la place
à la place 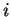 , un
, un 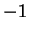 à la place
à la place 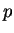 et des 0 ailleurs. Dans cette base,
et des 0 ailleurs. Dans cette base, 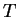 est représenté par la matrice
est représenté par la matrice
En notant que la somme des éléments d'une ligne de la matrice de droite vaut toujours 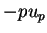 et en tenant compte du fait que le produit des
et en tenant compte du fait que le produit des 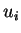 vaut
vaut 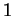 , on vérifie facilement que le déterminant du produit ci-dessus est égal à
, on vérifie facilement que le déterminant du produit ci-dessus est égal à
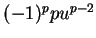 .
.
Compte tenu de ce qui précède, on en déduit immédiatement la valeur annoncée pour la courbure de Gauss 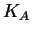 .
.
Celle-ci atteint une valeur extrême lorsque
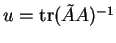 fait de même. La nature de cet extremum dépend de
fait de même. La nature de cet extremum dépend de 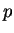 qui conditionne le signe de
qui conditionne le signe de 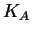 . En fait, en vertu de l'inégalité entre la moyenne arithmétique et la moyenne géométrique,
. En fait, en vertu de l'inégalité entre la moyenne arithmétique et la moyenne géométrique,
l'égalité ayant lieu si et seulement si les 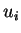 sont égaux, à
sont égaux, à 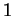 . Ceci arrive exactement quand
. Ceci arrive exactement quand
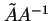 est la matrice unité, c'est-à-dire quand
est la matrice unité, c'est-à-dire quand 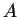 est orthogonal.
est orthogonal.



suivant: 7 Inégalité isopérimétrique
monter: 6.2.4 Courbure de Gauss
précédent: 6.2.4 Courbure de Gauss
Table des matières
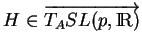 . On obtient ainsi facilement l'application de Weingarten de
. On obtient ainsi facilement l'application de Weingarten de
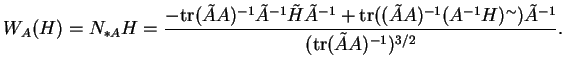
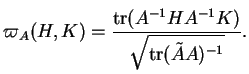
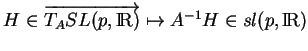 , on obtient
, on obtient
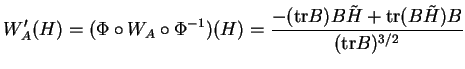
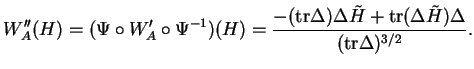
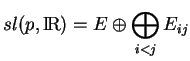
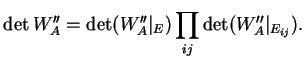
![]() ,
, ![]() est formé des matrices
est formé des matrices ![]() de trace nulle dont les éléments
de trace nulle dont les éléments
![]() , sont nuls.
C'est un espace de dimension
, sont nuls.
C'est un espace de dimension ![]() admettant une base
admettant une base ![]() , où
, où
![]() et
et
![]() . Dans celle-ci, la restriction de
. Dans celle-ci, la restriction de ![]() à
à ![]() est représentée par la matrice
est représentée par la matrice
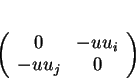
![]() est formé des matrices diagonales
est formé des matrices diagonales
![]() de trace nulle. Il admet la base
de trace nulle. Il admet la base
![]() dans laquelle
dans laquelle ![]() a un
a un ![]() à la place
à la place ![]() , un
, un ![]() à la place
à la place ![]() et des 0 ailleurs. Dans cette base,
et des 0 ailleurs. Dans cette base, ![]() est représenté par la matrice
est représenté par la matrice
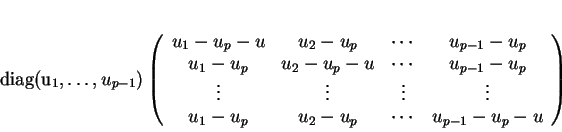
![]() .
.
![]() fait de même. La nature de cet extremum dépend de
fait de même. La nature de cet extremum dépend de ![]() qui conditionne le signe de
qui conditionne le signe de ![]() . En fait, en vertu de l'inégalité entre la moyenne arithmétique et la moyenne géométrique,
. En fait, en vertu de l'inégalité entre la moyenne arithmétique et la moyenne géométrique,