


suivant: 4.3 La sphère ,
monter: 4 Quelques cas particuliers
précédent: 4.1 Une quadrique:
Table des matières
La correspondance
transforme le produit de nombres complexes en le produit matriciel.
En effet, la matrice 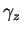 repésente la multiplication
repésente la multiplication
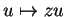 par
par 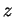 dans la base
dans la base
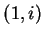 de
de
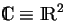 et, comme la multiplication dans
et, comme la multiplication dans
 est associative, on a
est associative, on a
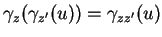 pour tout
pour tout 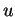 .
Dans cette correspondance, les nombres réels
.
Dans cette correspondance, les nombres réels 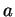 sont associés aux
multiples
sont associés aux
multiples 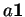 de l'identité. De plus,
de l'identité. De plus,
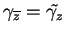 . En
particulier,
. En
particulier,
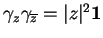 . Ainsi, si
. Ainsi, si 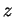 est de
module
est de
module 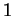 alors
alors 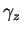 est une rotation. Il est facile de
vérifier que la réciproque est
vraie: toute rotation plane est représentée par une matrice de la
forme
est une rotation. Il est facile de
vérifier que la réciproque est
vraie: toute rotation plane est représentée par une matrice de la
forme 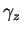 , avec
, avec 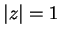 .
.
Les nombres complexes de module 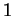 correspondent donc exactement aux
matrices de rotation: le groupe des rotations planes,
correspondent donc exactement aux
matrices de rotation: le groupe des rotations planes, 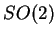 ,
est
isomorphe à la circonférence
,
est
isomorphe à la circonférence 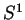 de centre 0 et de rayon
de centre 0 et de rayon 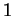 contenue dans
contenue dans
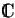 , considérée comme groupe pour la multiplication
des nombres complexes.
, considérée comme groupe pour la multiplication
des nombres complexes.
Lorsque 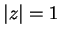 ,
,
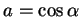 et
et
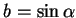 pour un certain
pour un certain
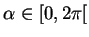 , argument de
, argument de 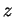 . C'est aussi une mesure de
l'angle de la rotation
. C'est aussi une mesure de
l'angle de la rotation
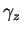 .
.



suivant: 4.3 La sphère ,
monter: 4 Quelques cas particuliers
précédent: 4.1 Une quadrique:
Table des matières
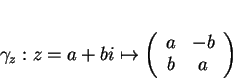
![]() correspondent donc exactement aux
matrices de rotation: le groupe des rotations planes,
correspondent donc exactement aux
matrices de rotation: le groupe des rotations planes, ![]() ,
est
isomorphe à la circonférence
,
est
isomorphe à la circonférence ![]() de centre 0 et de rayon
de centre 0 et de rayon ![]() contenue dans
contenue dans
![]() , considérée comme groupe pour la multiplication
des nombres complexes.
, considérée comme groupe pour la multiplication
des nombres complexes.
![]() ,
,
![]() et
et
![]() pour un certain
pour un certain
![]() , argument de
, argument de ![]() . C'est aussi une mesure de
l'angle de la rotation
. C'est aussi une mesure de
l'angle de la rotation
![]() .
.