



suivant: 3.1.2 Classification des quadriques
monter: 3.1 Les quadriques
précédent: 3.1 Les quadriques
Table des matières
Une quadrique de
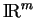 est l'ensemble des points de
est l'ensemble des points de
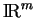 annulant un polynôme du second degré. Un tel polynôme s'écrit toujours sous la forme
annulant un polynôme du second degré. Un tel polynôme s'écrit toujours sous la forme
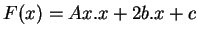 , où
, où 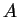 est une application linéaire symétrique (c'est-à-dire telle que
est une application linéaire symétrique (c'est-à-dire telle que 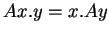 pour tous
pour tous
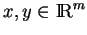 ), non nulle,
), non nulle,
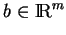 et
et
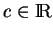 . On a
. On a
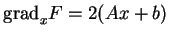 .
.
Proposition 11
Les points

vérifiant
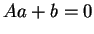
sont des centres de symétrie de la quadrique
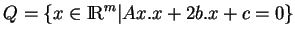
.
Soit 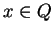 . Son symétrique par rapport à
. Son symétrique par rapport à  est
est 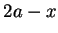 . On a
. On a
En raison de cette propriété, on dit que les solutions de 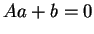 sont des centres de la quadrique
sont des centres de la quadrique 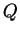 . Il en existe si
. Il en existe si
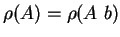 .
.
Les ellipses, les hyperboles ont exactement un centre chacune. Les paraboles en sont dépourvues. Les ellipsoïdes et les hyperboloïdes ont également un centre chacun, les paraboloïdes en sont dépourvus. Les cylindres elliptiques ou hyperboliques ont une droite de centre, etc.
Une quadrique dont on retire les centres éventuels est donc une variété plongée de codimension  .
.
Lemme 12
Une droite qui rencontre une quadrique en trois points distincts est tout entière contenue dans celle-ci.
Les points d'intersection de la droite passant par
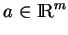 et parallèle à
et parallèle à 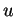 , avec la quadrique
, avec la quadrique
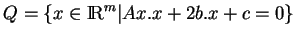 sont les points
sont les points 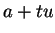 , où
, où 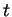 décrit les solutions de l'équation
c'est-à-dire
décrit les solutions de l'équation
c'est-à-dire
Si elle n'est pas identiquement nulle, celle-ci admet au plus deux solutions.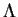
Une quadrique qui contient un de ses centres est un cône dont celui-ci est un sommet.
Un cône est une union de droites ayant un point commun, appelé sommet du cône. Ces droites sont les génératrices du cône.
L'ensemble des solutions d'un système d'équations homogènes
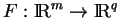 est un cône de
est un cône de
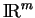 dont l'origine est un sommet. En effet, s'il contient
dont l'origine est un sommet. En effet, s'il contient  , il contient aussi les multiple de
, il contient aussi les multiple de  , en raison de l'homogénéité des équations.
Un cône peut avoir plusieurs sommets. Par exemple, l'union de deux plans sécants de
, en raison de l'homogénéité des équations.
Un cône peut avoir plusieurs sommets. Par exemple, l'union de deux plans sécants de
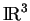 est un cône dont les sommets sont les points de l'intersection des plans.
est un cône dont les sommets sont les points de l'intersection des plans.
Proposition 13
Soit un centre

d'une quadrique
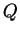
. Si
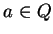
, alors toute droite qui passe par

et qui rencontre
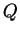
en un autre point est tout entière contenue dans
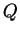
.
En effet,  étant un centre de symétrie de
étant un centre de symétrie de 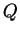 , une droite passant par
, une droite passant par  et rencontrant
et rencontrant 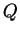 en un autre point passe aussi par un troisième point de
en un autre point passe aussi par un troisième point de 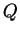 , son symétrique par rapport à
, son symétrique par rapport à  .
.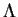
A cause de cette propriété, les centres d'une quadrique qui lui appartiennent sont appelés points doubles.
Pour la quadrique
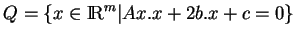 ce sont les solutions du système d'équations
ce sont les solutions du système d'équations
S'il en existe, le déterminant 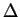 de
est nul. Les coniques pour lesquelles ceci est vérifié sont des couples de droites. Lorsqu'elles sont sécantes, elles se coupent en un point double. Lorsqu'elles sont confondues, tous leurs points sont doubles. Dans
de
est nul. Les coniques pour lesquelles ceci est vérifié sont des couples de droites. Lorsqu'elles sont sécantes, elles se coupent en un point double. Lorsqu'elles sont confondues, tous leurs points sont doubles. Dans
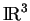 , deux plans sécants ont une droites de points doubles, etc.
, deux plans sécants ont une droites de points doubles, etc.
Il peut arriver que 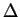 soit nul sans que
soit nul sans que 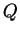 ait des points doubles. C'est le cas
par exemple de deux droites parallèles.
ait des points doubles. C'est le cas
par exemple de deux droites parallèles.




suivant: 3.1.2 Classification des quadriques
monter: 3.1 Les quadriques
précédent: 3.1 Les quadriques
Table des matières
![]() .
.
est un cône de
dont l'origine est un sommet. En effet, s'il contient
, il contient aussi les multiple de
, en raison de l'homogénéité des équations. Un cône peut avoir plusieurs sommets. Par exemple, l'union de deux plans sécants de
est un cône dont les sommets sont les points de l'intersection des plans.
![]() ce sont les solutions du système d'équations
ce sont les solutions du système d'équations
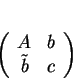
![]() soit nul sans que
soit nul sans que ![]() ait des points doubles. C'est le cas
par exemple de deux droites parallèles.
ait des points doubles. C'est le cas
par exemple de deux droites parallèles.