



suivant: 2.2.1 Définition
monter: 2 Définition des variétés
précédent: 2.1.3 Equivalence
Table des matières
Soit un paramétrage
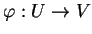 . La relation
caractérise les points de
. La relation
caractérise les points de  . L'élimination de
. L'élimination de 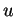 consiste à exprimer les conditions nécessaires et suffisantes que les coordonnées de
consiste à exprimer les conditions nécessaires et suffisantes que les coordonnées de 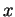 doivent satisfaire pour qu'il vérifie cette relation, c'est-à-dire pour qu'il appartienne à
doivent satisfaire pour qu'il vérifie cette relation, c'est-à-dire pour qu'il appartienne à  . On s'attend à ce qu'elles prennent la forme d'équations
. On s'attend à ce qu'elles prennent la forme d'équations
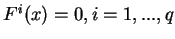 , éventuellement assorties de conditions précisant les domaines de définitions des fonctions
, éventuellement assorties de conditions précisant les domaines de définitions des fonctions 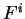 . Inversement, la résolution de ces équations consiste à fournir une description expicite de leurs solutions. Lorsqu'il y a moins d'équations que d'inconnues, on peut présumer que celles-ci dépendent d'un certain nombre de paramètres.
. Inversement, la résolution de ces équations consiste à fournir une description expicite de leurs solutions. Lorsqu'il y a moins d'équations que d'inconnues, on peut présumer que celles-ci dépendent d'un certain nombre de paramètres.
Sous-sections