suivant: 2.1.3 Equivalence
monter: 2.1 Paramétrages
précédent: 2.1.1 Définition
Table des matières
On obtient une famille importante de paramétrages en considérant des fonctions et leur graphes. Si
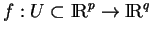 est de classe
est de classe 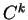 , alors
est un paramétrage du graphe
, alors
est un paramétrage du graphe
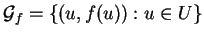 de
de  . Il est évident que c'est une bijection de
. Il est évident que c'est une bijection de 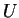 sur
sur
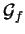 et qu'elle est de classe
et qu'elle est de classe 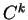 .
.
L'application réciproque
est continue comme on le voit directement en appliquant la Proposition 2. C'est en effet la restriction de l'application différentiable
Comme
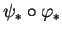 est donc injectif,
est donc injectif,  est de rang
est de rang 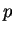 . Cela se voit aussi sur la matrice représentant
. Cela se voit aussi sur la matrice représentant
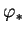 , à savoir
dont les
, à savoir
dont les 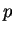 premières lignes forment un mineur non nul. Le paramétrage
premières lignes forment un mineur non nul. Le paramétrage  est un paramétrage par des coordonnées. Ce sont en effet certaines coordonnées qui servent de paramètres. Dans l'exemple qui vient d'être détaillé, il s'agit des
est un paramétrage par des coordonnées. Ce sont en effet certaines coordonnées qui servent de paramètres. Dans l'exemple qui vient d'être détaillé, il s'agit des 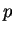 premières. Mais il peut s'agir de n'importe lesquelles. Ainsi, pour paramétrer le cercle de centre
premières. Mais il peut s'agir de n'importe lesquelles. Ainsi, pour paramétrer le cercle de centre 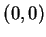 et de rayon
et de rayon 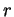 dans
dans
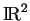 , on est amené à considérer non seulement les paramétrages
, on est amené à considérer non seulement les paramétrages
![$ x\mapsto\pm\sqrt{r^2-x^2}, x\in]-r,r[,$](img282.gif) mais également les paramétrages
mais également les paramétrages
![$ y\mapsto\pm\sqrt{r^2-y^2},y\in]-r,r[$](img283.gif) .
.




suivant: 2.1.3 Equivalence
monter: 2.1 Paramétrages
précédent: 2.1.1 Définition
Table des matières