suivant: 1.2 Applications différentiables
monter: 1.1.3 Application continue
précédent: 1.1.3.2 Application continue
Table des matières
Voici deux propriétés permettant de vérifier facilement qu'une application
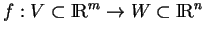 est continue.
est continue.
Proposition 2
Une application
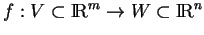
est continue si, pour tout
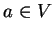
, il existe un ouvert
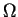
de
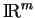
contenant

et une application continue
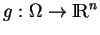
tels que
Soit un ouvert 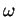 de
de 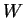 . C'est l'intersection de
. C'est l'intersection de 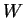 avec un ouvert
avec un ouvert 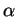 de
de
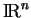 . Soient
. Soient
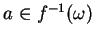 et
et 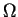 ,
, 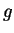 comme dans l'énoncé. On a
L'ensemble
comme dans l'énoncé. On a
L'ensemble
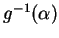 est un ouvert de
est un ouvert de
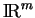 car
car 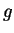 est continu. Par conséquent,
est continu. Par conséquent,
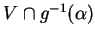 est un ouvert de
est un ouvert de  . Il en va de même de
. Il en va de même de
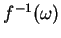 qui est une union de tels ouverts.
qui est une union de tels ouverts.
Proposition 3
Une application
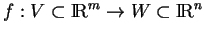
est continue si pour tout
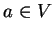
et pour toute suite
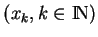
de points de

qui converge vers

dans
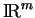
, la suite
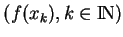
converge vers
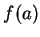
dans
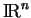
.
a) Supposons  continu. Soient
continu. Soient 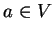 et une suite
et une suite
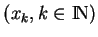 de points de
de points de  qui converge vers
qui converge vers  dans
dans
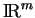 . Soit
. Soit
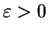 . L'ensemble
est un ouvert de
. L'ensemble
est un ouvert de 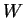 . Par conséquent,
. Par conséquent,
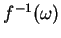 en est un de
en est un de  , contenant
, contenant  . Il existe donc un ouvert
. Il existe donc un ouvert 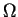 de
de
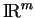 tel que
tel que
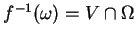 . Puisque
. Puisque 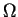 est une union de boules de
est une union de boules de
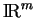 , il existe
, il existe 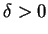 tel que
Pour
tel que
Pour 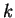 assez grand,
assez grand,
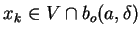 et, donc
et, donc
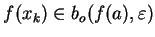 . La suite
. La suite
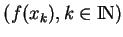 converge donc vers
converge donc vers 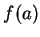 dans
dans
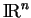 .
.
b) Inversement, supposons que pour tout 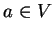 et pour toute suite
et pour toute suite
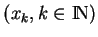 de points de
de points de  qui converge vers
qui converge vers  dans
dans
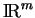 , la suite
, la suite
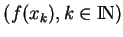 converge vers
converge vers 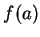 dans
dans
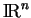 et montrons que
et montrons que  est continu. Soit un ouvert
est continu. Soit un ouvert
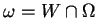 de
de 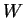 . Pour montrer que
. Pour montrer que
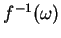 est ouvert dans
est ouvert dans  , on va vérifier que pour tout
, on va vérifier que pour tout
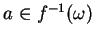 , il existe
, il existe 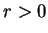 tel que
tel que
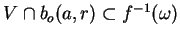 .
.
Il s'en suivra que
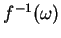 est ouvert, comme intersection de
est ouvert, comme intersection de  et de l'ouvert de
et de l'ouvert de
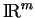 formé de l'union des boules ainsi récoltées.
formé de l'union des boules ainsi récoltées.
Procédons par l'absurde et supposons qu'il existe 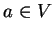 tel que
tel que
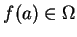 et tel que pour tout
et tel que pour tout 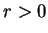 , il existe
, il existe
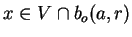 tel que
tel que
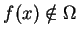 . En prenant
. En prenant
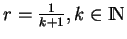 , on obtient une suite
, on obtient une suite
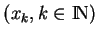 de points de
de points de  telle que
D'où la contradicition car cette suite converge vers
telle que
D'où la contradicition car cette suite converge vers  dans
dans
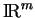 mais
mais
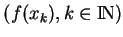 ne converge pas vers
ne converge pas vers 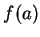 dans
dans
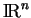 .
.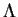




suivant: 1.2 Applications différentiables
monter: 1.1.3 Application continue
précédent: 1.1.3.2 Application continue
Table des matières
![]() est continue.
est continue.
![]() et pour toute suite
et pour toute suite
![]() de points de
de points de ![]() qui converge vers
qui converge vers ![]() dans
dans
![]() , la suite
, la suite
![]() converge vers
converge vers ![]() dans
dans
![]() et montrons que
et montrons que ![]() est continu. Soit un ouvert
est continu. Soit un ouvert
![]() de
de ![]() . Pour montrer que
. Pour montrer que
![]() est ouvert dans
est ouvert dans ![]() , on va vérifier que pour tout
, on va vérifier que pour tout
![]() , il existe
, il existe ![]() tel que
tel que
![]() .
.
est ouvert, comme intersection de
et de l'ouvert de
formé de l'union des boules ainsi récoltées.