



suivant: 1.2.5 Gradient
monter: 1.2 Applications différentiables
précédent: 1.2.3 Rang d'une application
Table des matières
L'expression du théorème de dérivation des fonctions composées en termes d'application linéaires est particulièrement élégante.
Proposition 6
Soient des ouverts
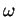
inclus dans
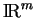
et
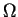
inclus dans
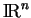
et des applications
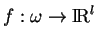
et
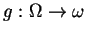
. Si

et
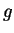
sont de classe
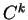
, avec
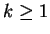
, alors
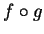
est de classe
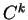
et, pour tout
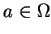
, on a